Da Psicopatologia strutturale e dialettica
Nota sulla "Teoria delle catastrofi”
Il riferimento, frequente nel testo, alla teoria delle catastrofi e l'adozione di concetti e termini propri di questa teoria, meritano una delucidazione.
Il modello psicopatologico struttural-dialettico è stato elaborato a partire dall'esperienza clinica senza alcuna preoccupazione originaria di formalizzazione. Solo in una fase avanzata, le analogie tra quel modello e la teoria delle catastrofi sono risultate evidenti. Le ovvie difficoltà di una valutazione quantitativa dei parametri in gioco nelle esperienze psicopatologiche impongono di considerare, per ora, tali analogie solo come suggestive. Esse, in breve, non consentono alcuna formalizzazione, pur corroborando la possibilità che il modello psicopatologico struttural-dialettico sia formalizzabile.
Ritenendo che la teoria delle catastrofi, non solo nei suoi aspetti matematici estremamente complessi, ma anche come metodologia e linguaggio, non debba necessariamente far parte dell'attrezzatura culturale del lettore, sembra opportuno fornire qualche indicazione a riguardo, al fine di evidenziare l'intima affinità tra tale teoria e la psicopatologia dinamica.
L'oggetto proprio della teoria delle catastrofi sono i sistemi complessi, intendendo con questo termine sistemi di qualsivoglia natura che siano anzitutto definibili in rapporto all'ambiente, che abbiano dunque una forma e risultino pertanto osservabili. La complessità è riconducibile al fatto che tali sistemi sono costituiti da un numero elevato di componenti, che interagiscono tra loro dinamicamente, assumendo, in conseguenza della gerarchia che s’instaura tra essi, configurazioni stabili e/o instabili. L'insieme delle interazioni dà origine ad un sistema dotato di significato, vale a dire di una struttura tale che un osservatore può sostituire una dettagliata descrizione di esse con un'altra, più compressa, che ne coglie alcuni aspetti essenziali.
Per la dinamica ad essi propria, i sistemi complessi, che ovviamente sono aperti all'ambiente, evolvono. La loro evoluzione riconosce, però, a differenza dei sistemi semplici, lineari, nei quali è dimostrato un rapporto causale tra continuità delle cause e continuità degli effetti, due fatti singolari: il primo è l'emergenza di strutture e livelli d’organizzazione qualitativamente diversi della somma delle parti, il secondo è il sopravvenire, imprevedibilmente, di bruschi salti qualitativi, di discontinuità che danno luogo alla riorganizzazione del sistema in una forma diversa rispetto a quella preesistente. La fenomenologia dei sistemi complessi si sottrae di conseguenza ad una spiegazione riduzionistica, necessariamente incentrata sul paradigma della continuità e postula una spiegazione strutturale, la definizione cioè di un numero finito di regole combinatorie concernenti alcune morfologie elementari il cui dispiegamento descrive la varietà fenomenica osservabile nell'evoluzione dei sistemi stessi. La teoria delle catastrofi, che intende fornire tale spiegazione, è, dunque, una teoria morfogenetica. Essa implica che le forme osservabili siano l'espressione di processi morfogenetici invisibili, dinamici e causali.
Tali processi sono riconducibili ad agenti di natura diversa a seconda del sistema, genericamente definibili come attrattori. L'equilibrio tra gli attrattori, che comporta una gerarchia dinamica tra gli stessi, coincide con una situazione di stabilità strutturale: situazione tale per cui piccoli cambiamenti di quell'equilibrio non modificano la forma del sistema. L'intensificarsi del conflitto tra gli attrattori determina invece una condizione d’instabilità strutturale: condizione di equiprobabilità tale per cui piccoli cambiamenti dello stato del sistema possono determinare una catastrofica riorganizzazione dello stesso in forme affatto diverse, contrassegnate da una diversa gerarchizzazione tra gli attrattori in gioco. Per ogni sistema si può definire dunque un ciclo-limite, intendendo con questo una dinamica tra gli attrattori che, fino ad un certo punto, che rappresenta il limite, appare compatibile con una determinata morfologia. Superato tale limite, l'instabilità strutturale produce la riorganizzazione fenomenologica del sistema stesso che avviene però secondo modalità che sono probabilistiche non deterministiche.
La catastrofe definisce un brusco cambiamento qualitativo nell'evoluzione del sistema, una discontinuità. Assumendo gli attrattori come variabili di controllo e la forma o il comportamento del sistema come variabile di stato, la teoria delle catastrofi, nella versione originale di R. Thom, descrive 7 morfologie elementari, in riferimento ad un numero di variabili di controllo da 1 a 4.
E' evidente che questo numero rappresenta il limite epistemologico più rilevante all'applicazione della teoria delle catastrofi nell'ambito delle scienze umane e sociali, laddove la complessità dei sistemi - si tratti di una personalità o di una comunità sociale - è tale da indurre a ritenere che le variabili siano molteplici. Posto, però, che l'obiettivo della scienza sia quello di ricondurre la complessità fenomenologica a matrici strutturali semplici, il gioco combinatorio tra le quali salda lo scarto tra forme osservabili e processi dinamici sottostanti invisibili, c'è da chiedersi se, nei sistemi complessi umani e sociali, non sia individuabile un numero ristretto di variabili morfogenetiche compatibili con la teoria delle catastrofi atte a funzionare come attrattori in rapporto all'insieme molteplici di variabili.
E' a questo punto che si definisce la possibilità di ricondurre il modello psicopatologico struttural-dialettico alla teoria delle catastrofi.
A livello neurobiologico - neuronale e neuroendocrino - e a livello psicodinamico - identificabile con la rete dei significati consci e inconsci che integrano emozionalità e cognizione -, il sistema mentale è indubbiamente caotico. L'ordine, quale che sia, assicurato dalla coscienza, espressa da un certo grado di coerenza nel sentire, nel pensare e nell'agire implica un qualche potere integrativo, strutturante dell'io cosciente, che va considerato dunque come una qualità emergente. A ben vedere, però, questo potere, che dà luogo alle forme dell'esperienza soggettiva, ad una fenomenologia in virtù della quale l'io s’identifica e viene identificato dagli altri, non potrebbe realizzarsi a partire dal caos. Esso, in breve, implica un processo morfogenetico nell'accezione propria della teoria delle catastrofi.
Dal punto di vista struttural-dialettico, tale processo riconosce come agenti dinamici o attrattori i programmi affettivo-cognitivi innati (bisogno di appartenenza/integrazione sociale, bisogno di opposizione/individuazione) che, dispiegandosi nel corso dell'evoluzione della personalità danno luogo a strutture psicobiologiche (rispettivamente il Super-Io e l’Io antitetico) che veicolano sistemi di significati o patterns - emozionali, cognitivi e comportamentali - specifici e in tensione dialettica. La tensione dialettica, conflittuale tra tali patterns - che rappresentano dunque gli assi strutturali della personalità - riconosce gradienti diversi, da un minimo ad un massimo, riconducibili alla storia del soggetto e alle circostanze di vita con cui interagisce.
Identificando gli assi strutturali della personalità con il dover essere inerente l'appartenenza e il voler essere inerente la libertà personale, e considerando che ciascuno di questi valori riconosce una rappresentanza conscia e un’inconscia non necessariamente integrate, riesce evidente che ogni personalità può essere identificata con un sistema complesso il cui comportamento - variabile di stato - esprime il potere integrativo dell'io sulle substrutture che lo sottendono che rappresentano le variabili di controllo.
Riesce anche evidente che quel potere dipende dai gradienti conflittuali - attuali e potenziali - intrinseci a tali sistemi. La stabilità strutturale della personalità esprime il fatto che tali gradienti oscillano dinamicamente entro un ciclo-limite compatibile con la forma dell'esperienza soggettiva, che non comporta discontinuità qualitativa. Se il conflitto s’intensifica, si realizza una condizione d’instabilità catastrofica che può evolvere, a seconda delle circostanze soggettive e ambientali, o nella direzione di un cambiamento rilevante del modo di essere e di porsi del soggetto o nella direzione di un cambiamento psicopatologico, che rende discontinua l'esperienza in conseguenza dell'affiorare di sintomi, vissuti e comportamenti che attestano il predominio dinamico di una substruttura - la funzione superegoica o l'io antitetico.
Da questo punto di vista, si sarebbe portati a pensare che un solo modello catastrofico - quello della cuspide, che riconosce due variabili di controllo e una variabile di stato - potrebbe descrivere l'universo psicopatologico. Assumendo la matrice strutturale ossessiva come matrice univoca di tale universo, sono portato a dare credito all'ipotesi di una catastrofe psicopatologica elementare. I processi morfogenetici psicopatologici, però, sono un po' più complessi in rapporto al fatto che le variabili di controllo riconoscono rappresentanze consce e inconsce non necessariamente integrate. In conseguenza di ciò, il numero di tali variabili dovrebbe essere portato a quattro.
Con ciò si rimarrebbe comunque nell'ambito descrittivo della teoria delle catastrofi. E' evidente che tali variabili comportano un insieme indefinito di combinazioni che spiegherebbe, in termini strutturali, la varietà fenomenica delle esperienze psicopatologiche.
Lo schema dispiega su due assi strutturali tale varietà, ma ha implicanze cliniche più rilevanti. E' facile estrapolarne, infatti, configurazioni costanti a livello fenomenologico: configurazioni riconducibili alla prevalenza dinamica di una funzione superegoica punitiva e repressiva, di una funzione superegoica riparativa e preventiva, di un io antitetico opposizionistico e negativista e di un io sfidante e rivendicativo.
Tali configurazioni stabili, in rapporto a piccoli cambiamenti delle variabili di controllo, possono anche fluttuare e virare catastroficamente.
Con ciò si è ancora ben lontani dalla formalizzazione. Si è, però, più vicini alla realtà clinica di qualunque altra impostazione a me nota e - rilievo di grande importanza - la si vede organizzata in maniera compressa, intelligibile e suggestivamente aperta ad ulteriori approfondimenti.
Psicopatologia dinamica struttural-dialettica e teoria delle catastrofi (novembre 2006)
1) Sistemi dinamici non lineari
Per sistema si intende un qualunque insieme di elementi o parti, diversi tra loro, tra i quali si danno connessioni.
Se le parti sono numerose, hanno un certo grado di autonomia, ma sono anche interdipendenti, si parla di sistema complesso.
Un sistema che evolve nel corso del tempo, assumendo configurazioni diverse che corrispondono a stati del sistema, si definisce dinamico.
Un sistema dinamico può essere lineare o non lineare.
Un sistema dinamico lineare è deterministico, governato cioè da leggi di causa-effetto che consentono di ricondurre tutti i suoi possibili stati a equazioni differenziali. Data una conoscenza delle variabili di stato in un determinato momento, si possono formulare previsioni certe sulla sua evoluzione.
Un sistema dinamico lineare è dunque predicibile: esso ha un ordine, che esclude cambiamenti imprevedibili, e una continuità, per cui i cambiamenti che intervengono sono quantitativi, vale a dire spiegabili in termini di causa-effetto.
Un sistema dinamico non lineare, viceversa, è indeterministico. Apparentemente esso sembra caotico, non governato da alcuna legge che consenta di operare previsioni certe, e caratterizzato da un’evoluzione che può comportare repentinamente discontinuità qualitative, vale a dire bruschi cambiamenti della sua forma che appaiono aleatori e inspiegabili.
Il carattere caotico di un sistema dinamico non lineare è solo apparente. Un’analisi sottile, infatti, del comportamento del sistema, nei suoi vari stati, ha posto in luce che, al di sotto del disordine caotico, si dà un ordine. Tale ordine è riconducibile alla nozione di attrattore, termine che sta ad indicare che il sistema tende (viene attratto) verso un modello di comportamento dinamico senza però ripetersi in modo identico.
All’interno della teoria dei sistemi dinamici non lineari, complessi o caotici, si è definita la teoria delle catastrofi. Per catastrofi si intendono momenti di passaggio (o biforcazioni) tra differenti stati di equilibrio in relazione a variazioni anche piccole di parametri di controllo del sistema. In questa accezione, molto distante dal senso comune, le catastrofi sono transizioni da uno ad un altro stato di equilibrio. Esse comportano la ristrutturazione del sistema, che spesso si manifesta attraverso un cambiamento della forma e del comportamento.
Date queste definizioni, non è sorprendente che la scienza, dai suoi esordi sino a qualche decennio fa, si sia dedicata allo studio dei sistemi dinamici lineari, e abbia trascurato, in quanto caotici, quelli non lineari. Si riteneva, insomma, che gran parte dei fenomeni naturali rientrassero nell’ambito del determinismo, e che, al di fuori di essi si desse solo un disordine non passibile di indagine scientifica. La causalità era privilegiata rispetto alla casualità, considerata accidentale.
Ci si è resi poi conto: primo, che in natura i sistemi dinamici non lineari sono a tal punto presenti che la realtà sembra configurarsi come un mare di indeterminismo nel quale si danno isole di determinismo; secondo, come accennato, che il disordine che governa quei sistemi è solo apparente. Le discontinuità qualitative, infatti, rappresentano il passaggio ad un’altra organizzazione dinamica del sistema, che si differenzia dalla precedente solo per la forma, gli elementi rimanendo gli stessi.
Si è perciò cominciato a parlare di caos deterministico, vale a dire di apparenze caotiche che danno luogo però ad evoluzioni riconducibili a leggi deterministiche. Il problema – che differenzia nettamente i sistemi dinamici non lineari rispetto a quelli lineari - è che quelle leggi valgono a descrivere i singoli stati che il sistema assume, ma non possono essere utilizzate per operare previsioni certe sulla sua evoluzione, che dunque è probabilistica, apparentemente casuale.
L’impredicibilità dei sistemi dinamici non lineari è riconducibile al fatto che piccole variazioni dei fattori di stato in un determinato momento possono produrre, nel corso del tempo, evoluzioni del tutto diverse.
Per quanto diverse, però, le possibili configurazioni di un sistema dinamico non lineare godono ciascuna di una certa stabilità, di una forma che sembra di fatto determinata, agganciata a “qualcosa” che la mantiene e dà ad essa ordine. Per definire questo “qualcosa” si utilizza il termine attrattore.
La non linearità di un sistema dipende dall’equilibrio dinamico dei suoi elementi. Tale equilibrio, in conseguenza del numero degli elementi e dell’interazione tra loro, può mantenersi a lungo stabile, ma può evolvere anche nella direzione dell’instabilità.
L’instabilità significa che la struttura e la forma che il sistema ha mantenuto sino allora diventano poco compatibili con la dinamica che si dà tra i suoi elementi, tra i quali occorre ammettere che sia intervenuto un conflitto.
Raggiunto uno stato di instabilità, un sistema complesso si trova di fronte a biforcazioni, vale a dire ad alternative che comportano il raggiungimento di un nuovo stato di stabilità strutturale attraverso un cambiamento di forma. Tali alternative sono però impredicibili, finché una di esse non si realizza.
E’ dunque l’instabilità di un sistema complesso a impedire l’applicazione ad esso di leggi deterministiche. Essa, infatti, comporta un’equiprobabilità di cambiamento che tale rimane finché il sistema non assume una nuova configurazione.
I cambiamenti che avvengono in un sistema complesso quando esso salta al di là di una biforcazione sono qualitativi: essi si manifestano con una discontinuità tale per cui la nuova forma che assume il sistema sembra più o meno diversa da quella che esso aveva in precedenza.
In breve, un sistema complesso non lineare oscilla perpetuamente tra l’equilibrio (stabilità) e il non equilibrio (instabilità), l’ordine e il disordine, il determinismo e l’indeterminismo. L’indizio di questa dinamica interna al sistema, che può apparire impercettibile, è la forma, la fenomenologia del sistema stesso, che può mantenersi per lungo tempo e poi repentinamente mutare in maniera imprevedibile e radicale.
2) Il cervello e la mente come sistemi dinamici non lineari
Che il cervello sia un sistema dinamico non lineare è fuor di dubbio. Basta pensare al fatto che esso è composto di cento miliardi di cellule che interagiscono tra loro in maniera tale che il funzionamento di ciascuna di esse dipende dalla somma degli stimoli che, attraverso le connessioni interneuronali, riceve da un numero indefinito di altre cellule (alle quali esso stesso invia stimoli).
Il comportamento di una singola cellula è stocastico, imprevedibile, poiché non è possibile quantificare gli stimoli che essa riceve e sapere in anticipo se essa è destinata a scaricare o meno un impulso.
Il cervello, dunque, è tipicamente un sistema caotico.
Al di là della possibilità di registrare (elettroencefalograficamente) l’attività cerebrale e di visualizzarla, sia pure in maniera grossolana, attraverso tecniche di neuroimaging, l’aspetto funzionale più importante di tale attività è il comportamento osservabile del soggetto.
Non appena si ascende nella scala animale e si va al di là del livello governato dal rapporto stimolo-risposta, prevedibile perché ha una matrice istintuale, ci si trova immediatamente di fronte alle prove che il cervello è un sistema dinamico non lineare.
Uno tra gli esempi più citati a riguardo concerne il comportamento del predatore di fronte alla preda. L’osservatore rileva ad un certo punto che esso è bloccato, come se fosse inibito (oltre che dalla paura) da una “decisione” da prendere. L’alternativa, ovviamente, è tra la lotta e la fuga. E’ scontato che uno dei due comportamenti è destinato a realizzarsi, ma la capacità previsionale dell’osservatore equivale al puntare sulla possibilità che, lanciando una moneta, compaia la testa o la croce. La situazione, insomma, è impredicibile.
Essa coincide, nel cervello dell’animale e nella sua esperienza vissuta, con uno stato di instabilità che si è instaurato in seguito al cambiamento delle variabili di stato. C’è da presumere, infatti, che egli fosse tranquillo prima di trovarsi nel raggio d’azione di un predatore. La comparsa del predatore destabilizza il sistema, che non può più mantenere lo stato preesistente di quiete o di riposo, ma determina una situazione di instabilità equiprobabile, che può virare repentinamente nella direzione della lotta o della fuga.
L’esempio è semplicissimo perché la lotta o la fuga come risposta alla presenza di un predatore sono due comportamenti che hanno una matrice istintuale. Se essi, al di sopra di un certo livello della scala animale, non si realizzano “automaticamente”, ciò dipende dal fatto che è intervenuta, in rapporto alla complessità dell’animale una valutazione emotiva e cognitiva della situazione che, evidentemente, aumenta il grado della sua libertà di scelta, ma paradossalmente la rende anche più difficile perché determina uno stato intermedio nel corso del quale, essendo le alternative equiprobabili (il che significa anche dinamicamente equivalenti), nessuna delle due si realizza.
A livello di massima complessità dell’organizzazione biologica, vale a dire a livello umano, il discorso è ancora più articolato.
Se si tiene conto, infatti, della caoticità dell’attività cerebrale, ciò che sembra immediatamente misterioso è il fatto che, su tale sfondo, si possa definire un Io cosciente che ha un senso di identità, unità e continuità.
Ponendo tra parentesi questo problema, di enorme portata, anche la forma del comportamento del singolo individuo – quella che con la sua iteratività definisce la sua personalità - non è priva di problemi.
In realtà, se si osserva con attenzione la condotta di un individuo, appare evidente che tra l’unità dell’Io e i comportamenti di fatto agiti si danno spesso, in misura più o meno rilevante, contraddizioni. Quello che l’individuo pensa di sé non corrisponde mai del tutto, anzi di solito corrisponde ben poco a ciò che egli pensa di essere.
Ciò nondimeno, sempre facendo riferimento alla caoticità del cervello, la fluidità media dei comportamenti individuali sembra abbastanza misteriosa. C’è da pensare che essa debba essere ricondotta, per un verso, a moduli comportamentali socialmente appresi (normativi) o abitudinari e per un altro a meccanismi di repressione/rimozione per cui il soggetto letteralmente non si accorge delle contraddizioni.
A livello umano, insomma, nonostante, sulla base dell’identificazione del cervello con un sistema dinamico non lineare, ci si potrebbe aspettare un’incidenza elevata di situazioni di instabilità e di discontinuità qualitative, ciò che sorprende è la bassa incidenza (almeno apparente) delle une e delle altre.
Ciò significa, né più né meno, che la coscienza funziona, in rapporto al cervello caotico, come un attrattore, che dà al sistema della personalità e al suo comportamento una qualche stabilità. Si tratta sempre e comunque di una stabilità relativa.
L’uomo è l’unico animale dotato di una doppia natura – sociale e individuale -, che fa capo a due logiche motivazionali (l’appartenenza e l’individuazione) sulla quale si definiscono due substrutture dell‘Io (il Super-Io e l’Io antitetico) che, in misura più o meno rilevante, sono in tensione dinamica tra loro, richiamando il soggetto per un verso al rispetto dei doveri sociali e per un altro alla realizzazione dei suoi bisogni e delle sue potenzialità individuali.
Pur tenendo conto dei codici normativi culturali, che tendono ad offrire canali atti a diminuire quella tensione, della capacità media di rimozione delle contraddizioni, che, al limite, le estinguono, e del grado di integrazione dell’Io, che svolge una funzione di mediazione, l’esistenza nell’uomo di una doppia natura e di elementi o parti che veicolano logiche motivazionali nettamente differenziate lascia pensare che le situazioni di instabilità strutturale siano, a livello inconscio, molto più frequenti di quanto appaia a livello di condotta cosciente.
Per questo aspetto, l’uomo, tenendo conto del cervello e dell’apparato mentale di cui dispone, è omologabile ad un sistema dinamico non lineare in grado per molti aspetti, legati alla struttura della coscienza, di “estinguere” gli effetti della complessità e della non linearità, vale a dire le discontinuità qualitative che comportano cambiamenti di forma (identificabile sul piano del comportamento). Può sembrare dunque (ed egli stesso indulge a pensarlo) un essere unitario, sostanzialmente ragionevole se non logico, il cui comportamento fluisce sulla base di nessi causali.
In realtà è un essere fatto di parti diverse, la cui ragionevolezza, nella maggioranza dei casi, si fonda sulla capacità di rimuovere le contraddizioni, e il cui comportamento si fonda su catene motivazionali del più vario genere, in gran parte inconsce.
Si dà dunque, in conseguenza della doppia natura e delle funzioni che su di essa si strutturano, una tensione conflittuale intrinseca alla soggettività umana.
3) Psicopatologia e teoria delle catastrofi. Un’esperienza clinica
La psicopatologia è l’ambito fenomenico attraverso cui quella tensione si rende manifesta secondo modalità che rientrano pienamente nell’ambito del caos deterministico. La teoria struttural-dialettica è il modello che cerca di spiegare – riuscendoci - l’aspetto caotico e quello deterministico dei fenomeni psicopatologici.
Per rendere immediatamente comprensibile questo assunto, parto da un esempio clinico.
A. è un bambino sensibile e intelligente, sicuramente introverso, che ha uno sviluppo di personalità abbastanza lineare: fa il suo dovere (senza eccellere, anche se, dall’adolescenza in poi, coltiva per conto proprio interessi culturali piuttosto inconsueti), non dà particolari problemi, ha un buon grado di integrazione sociale con i coetanei (particolarmente con alcuni). Nel suo assetto di personalità, a posteriori, è facilmente riconoscibile un’eccessiva soggezione nei confronti delle autorità, a partire dai genitori, che sono (più o meno consapevolmente) esigenti e severi.
Ciò nonostante, A. giunge all’ultimo anno di liceo senza manifestare problemi particolari (anche se è già seguito da uno psicologo per la sua “timidezza” poco compatibile con le aspettative genitoriali di un figlio del tutto normale). All’inizio dell’anno, si realizza una brusca discontinuità qualitativa della sua esperienza, sotto forma di un delirio di riferimento sotteso da vissuti persecutori. A. non solo si sente spesso osservato e giudicato negativamente dagli altri nelle più varie situazioni, egli avverte anche “nell’aria” oscure minacce che appaiono incomprensibili.
Con una cura di neurolettici, la situazione clinica rientra rapidamente, apparentemente senza lasciare traccia alcuna.
Un secondo episodio, più o meno con le stesse caratteristiche, si realizza ad un mese di distanza dagli esami. A differenza della prima volta, A. appare, oltre che bloccato dalle angosce persecutorie, smarrito, disorientato, confuso, disarticolato.
Riesce comunque a dare gli esami con esito positivo (grazie alla comprensione degli insegnati e ad una certificazione medica). Successivamente, sembra recuperare di colpo il suo assetto comportamentale preesistente di ragazzo normale.
Al rientro dalle vacanze, la situazione però precipita. A. cade in uno stato psicotico che lo inebetisce, impedendogli quasi di parlare. Visibile è l’angoscia che lo attanaglia e lo incupisce, al di sotto della quale si intuiscono vissuti persecutori. Si iscrive all’università, ma non riesce a frequentarla.
Si chiude in casa e si avvia una lunga stagione di malessere caratterizzata da due diversi moduli di comportamento.
Per un verso, A. è perennemente allarmato dalla possibilità di provare dolore e che qualcuno possa fargli del male. Coscientemente afferma di rifiutare la sofferenza e di aver deciso di mettersi al riparo da ogni possibilità di soffrire. E’ chiaro che convive con un’aspettativa del male che ha un significato inequivocabile: si sente in colpa per la sua inadempienza, per non essere più un bravo figlio, per il suo fare nulla dalla mattina alla sera, e vive temendo che sopravvenga la giusta punizione.
Per un altro aspetto, egli rifugge sistematicamente qualunque impegno, qualunque responsabilità. Vive in casa senza offrire alcuna collaborazione, si alza la mattina sul tardi, si distrae ascoltando musica a pieno volume. Per di più, egli è preda di una pulsione alla fuga per cui ogni tanto si allontana da casa, vaga per la città fino a tarda notte, qualche volta addirittura sale su di un treno andando alla ventura. Il suo comportamento sociale fuori casa è caratterizzato dal venir meno di qualunque vergogna, dall’agire come se non gli importasse nulla del giudizio degli altri, nel violare le regole della comune convivenza. Si espone, insomma, a rischi di ogni genere, e più volte viene ricondotto a casa dalla polizia.
L’esperienza di A. si iscrive nell’ambito delle psicosi giovanili, e implica evidentemente una perdita di controllo dell’Io su di un mondo interiore che è passato da una quiete apparente – quella che ha governato la vita di A. sino a 17 anni -, ad una sorta di repentina eruzione vulcanica (coincidente con i due deliri persecutori rapidamente regrediti), approdando infine ad una condizione al di sotto della quale occorre ammettere uno stato di turbolenza pressoché continuo.
Lo stato di turbolenza in questione è riconducibile a due diverse spinte motivazionali: l’una, che si esprime attraverso un livello di estrema colpevolizzazione, è orientata chiaramente a ricondurre A. sulla retta via, a farlo ridiventare il bravo ragazzo che è stato; l’altra, invece, che si esprime attraverso il disimpegno, la deresponsabilizzazione, l’inadempienza, le fughe all’impazzata, la violazione delle regole della civile convivenza, esprime un bisogno di libertà totale da qualunque vincolo, regola, soggezione.
Ricondurre la prima spinta motivazionale all’attività del Super-io, che ha governato l’esperienza di A. per lungo tempo, e la seconda ad un bisogno di opposizione/individuazione che, non essendosi mai espresso a livello cosciente, si è organizzato a livello inconscio sotto forma di un Io antitetico ribelle, anarchico e sfidante, sembra quasi ovvio.
Se ci riconduciamo al modello della teoria delle catastrofi la dinamica dell’esperienza diventa chiara in tutti i suoi aspetti.
La strutturazione della personalità di A. è evoluta e si è mantenuta per anni sul registro dell’autodirezione, vale a dire di un Super-Io interiorizzato, e potenziato al tempo stesso dalla sensibilità sociale e dalla paurosità di A., che ha impedito l’affiorare di qualsivoglia istanza oppositiva e individuante. Questo regime interiore ha assicurato una stabilità della personalità addirittura eccessiva in rapporto alla media: un’evoluzione, dunque, lineare e ipernormativa.
Esso, però, ha determinato anche l’accumulo dei potenziali frustrati legati al bisogno di individuazione che ha dato luogo allo strutturarsi, a livello inconscio, di un Io antitetico animato da una spinta rivendicativa di libertà la quale, crescendo nel corso del tempo, ha assunto una configurazione anarchica.
L’apparente normalità della personalità conteneva dunque già un potenziale di instabilità.
L’avvio dell’ultimo anno di liceo, come accade spesso in circostanze del genere, ha evocato in A. l’aspettativa che il conseguimento del diploma inaugurasse l’era della libertà che, a livello inconscio, data la struttura dell’Io antitetico, si è definita sotto forma di disimpegno e di inadempienza. Impattando contro una struttura superegoica ancora potente, le fantasie di un cambiamento radicale di vita – dal regime di soggezione normativa a quello di anarchia - hanno attivato, in seguito ad un processo di colpevolizzazione, i due episodi deliranti a contenuto persecutorio, evidentemente espressivi di un bisogno inconscio di punizione.
Le spinte libertarie, in altri termini, sono rimaste intrappolate dal Super-Io, che ha funzionato come attrattore, restaurando, dopo una sventagliata di colpevolizzazione, l’equilibrio strutturale preesistente.
Dopo il conseguimento del diploma, l’attività dell’Io antitetico si è incrementata, producendo una spinta pressoché continua nella direzione della fuga e della libertà (una libertà ovviamente immaginaria). Si è realizzato anche un disimpegno totale di A., che ha rifiutato di frequentare l’università, di dedicarsi ad una qualunque attività significativa e di dare ordine alla sua vita.
L’io antitetico si è posto dunque come un nuovo attrattore la cui attività dinamica si è “dissociata” rispetto a quella del Super-Io.
Tra Super-Io e Io antitetico si è instaurato, di conseguenza, un circolo vizioso dinamico: la persecuzione legata ai sensi di colpa e alle minacce punitive ha spinto A. a difendersi incrementando i livelli di distrazione e di disimpegno attraverso la fuga nel sonno di giorno e la fuga da casa di notte.
Il Super-Io e l’Io antitetico sono giunti insomma a funzionare come due variabili che, non riuscendo a prevalere dinamicamente l’una sull’altra, hanno determinato uno stato di instabilità dinamica caratterizzata da una continua fluttuazione del comportamento di A. tra il registro del senso di colpa e della paura e il registro della ribellione e della sfida, vale a dire tra due attrattori che, irretendo l’esperienza di A., impediscono sia il ricomporsi dell’equilibrio comportamentale preesistente sia il manifestarsi di un nuovo equilibrio.
L’esperienza di A. è dunque dissociata a livello comportamentale, ma si tratta di una dissociazione dinamica, che rientra a pieno titolo nella teoria delle catastrofi.
4. Psicopatologia e teoria delle catastrofi. Altre considerazioni
E’ evidente che le esperienze psicotiche, quando fanno affiorare a livello di superficie comportamentale i sintomi evidenti di una dissociazione dinamica tra parti (le substrutture dell’Io), sono le più facili da modellizzare.
Io penso che la teoria delle catastrofi possa essere impiegata per spiegare gran parte dei fenomeni psicopatologici. Un’illustrazione di questa convinzione richiederebbe un libro a parte.
Per ora, mi limito a fornire due esempi sganciati da storie cliniche, ma facenti capo a sintomi piuttosto frequenti.
Il primo esempio concerne i comportamenti contraddittori di soggetti femminili, affetti da una struttura isterica, nell’interazione con il partner. Tali comportamenti, per un verso, sono caratterizzati da una dipendenza più o meno rilevante, che, in casi estremi, giunge a forme di autentico aggrappamento, associata a richieste continue di conferme, a dubbi ricorrenti sull’affidabilità del partner, che si traducono spesso nell’angosciosa aspettativa di un abbandono dato per certo e concorrono ad incrementare quelle richieste. Isolando dal contesto del comportamento questi comportamenti, l’impressione, spesso esplicitata dai soggetti, è quella di un bisogno disperato di amore e di sicurezza che potrebbe essere soddisfatto solo in virtù di un rapporto chiuso ed esclusivo.
Per un altro verso, però, si danno anche comportamenti di segno opposto. Già l’aggrappamento, quando giunge ad essere asfissiante, nonostante le intenzioni coscienti dei soggetti, sembra mirato a determinare una situazione insopportabile per il partner, a provocarne dunque l’allontanamento. Al di là di questo, è frequente che sopravvengano, giustificati dalla frustrazione di aspettative non corrisposte, attacchi più o meno violenti – verbali e fisici – nei confronti di quegli. Tali attacchi vanno, inoltre, incontro ad un’escalation paradossale. Se il partner, infatti, interagisce comprendendo, tollerando e confermando la sua volontà di rimanere in rapporto, essi si incrementano esponenzialmente. Valutati sul piano oggettivo, gli attacchi sembrano denotare la volontà inconsapevole di obbligare il partner all’abbandono.
Allorché si giunge all’estremo e l’abbandono viene minacciato, gli attacchi regrediscono e vengono sostituiti da richieste imploranti di proseguire il rapporto, da aggrappamenti patetici, da promesse di tenere sotto controllo la rabbia, ecc.
Di fatto, la minaccia consegue l’effetto di riorganizzare il comportamento interattivo su di un registro spesso equilibrato. Il problema è che, nel corso del tempo, il ciclo si ripete con le stesse modalità.
E’ evidente in questi casi che sono in gioco due attrattori: l’uno che induce la regressione in una dipendenza estrema, che dà al perpetuarsi del rapporto un significato di vita o di morte; l’altro che sembra orientato ad affrancare il soggetto dalla dipendenza costringendo il partner all’abbandono.
L’altro esempio riguarda i rituali ossessivi, e in particolare quelli la cui esecuzione talora richiede un tempo smisurato. L’analisi di questi rituali pone di fronte al fatto che le procedure comportamentali che essi prescrivono sono piuttosto complesse e apparentemente irrazionali. Nel corso dell’esecuzione, anche se il soggetto sa perfettamente cosa deve fare, egli incorre in un errore che richiede la ripetizione del rituale. Il numero di errori che si ripetono talora è tale che il soggetto impiega ore per portare a termine un comportamento che, sulla carta, potrebbe essere realizzato in pochi minuti.
In questo caso, è evidente che l’esecuzione del rituale corrisponde ad un’imposizione superegoica il cui scopo è di piegare la volontà del soggetto al rispetto assoluto di regole, siano pure esse arbitrarie. L’ansia con cui il soggetto avvia l’esecuzione del rituale attesta la sua soggezione per paura alla minaccia implicita nell’imposizione di qualcosa di male che potrebbe accadergli in caso di inadempienza. L’errore che interviene sistematicamente è evidentemente l’espressione di una volontà oppositiva e ribelle, espressiva di un Io antitetico.
La soggezione e la ribellione che si succedono fino alla fine dell’esecuzione del rituale pone in luce l’esistenza di due attrattori entrambi dinamicamente attivi.
Mi auguro con questi esempi di avere illustrato la possibilità di formalizzare la teoria struttural-dialettica in riferimento al modello offerto dalla Teoria delle catastrofi.
Sarebbe ingenuo non aggiungere che si tratta di una formalizzazione suggestiva, che urta contro un limite forse invalicabile: l’impossibilità di quantificare le variabili di stato in questione. L’intensità dell’attività del Super-Io e dell’Io antitetico possono essere intuitivamente ricavate dagli effetti psicopatologici che esse producono, ma non si dà, almeno per ora, alcuna possibilità di ricondurle ad una scala di misura.
Comunque anche la sola analogia tra una teoria psicopatologica dinamica e un modello matematico è degna del massimo interesse.
Appendici matematiche
<
Negli ultimi venti anni, si è parlato molto dei metodi e dei risultati matematici che hanno portato alla definizione di caos deterministico. Questi risultati sono stati ottenuti nell'ambito di quel settore della Matematica noto come Teoria qualitativa dei sistemi dinamici e sono stati stimolati dall'esigenza di rappresentare, mediante modelli matematici, i sistemi reali che evolvono nel tempo come il moto dei pianeti, le oscillazioni di un pendolo, il flusso delle correnti atmosferiche, lo scorrere più o meno regolare dell'acqua in un fiume, il numero di insetti che anno dopo anno popolano una certa regione, l'andamento giornaliero dei prezzi delle azioni nei mercati finanziari e così via.
L'apparente contraddizione (o paradosso) contenuto nel termine caos deterministico, ha molto incuriosito anche il pubblico dei non specialisti. I modelli matematici di tipo deterministico vengono in genere associati all'idea di fenomeni regolari, prevedibili, che si ripetono nel tempo, mentre il termine caotico viene riferito a situazioni caratterizzate da assenza di regole e da imprevedibilità. La scoperta del caos deterministico spezza questa dicotomia, in quanto mostra come modelli matematici deterministici (cioè privi di ogni elemento aleatorio nelle equazioni che li definiscono) sono in grado di generare andamenti estremamente complessi, sotto molti aspetti imprevedibili, tanto da risultare quasi indistinguibili da sequenze di eventi generati attraverso processi aleatori.
Scopo di questo articolo è di descrivere a grandi linee lo sviluppo storico e introdurre un minimo di terminologia della teoria dei sistemi dinamici, facendo in particolare riferimento alla sua trattazione più moderna, nota come qualitativa (o topologica).
La teoria dei sistemi dinamici è stata anche chiamata la Matematica del tempo. In effetti, anche nel linguaggio comune, il termine dinamico si riferisce a processi che producono cambiamenti, ossia evolvono nel corso del tempo. Cerchiamo quindi di capire come si può simulare, matematicamente, l'evoluzione temporale di un sistema reale.
Innanzi tutto, occorre individuare un certo numero di grandezze misurabili, cioè espresse mediante numeri reali x1, x2, ..., xn, che permettano di identificare lo stato ossia la configurazione ad un certo istante t, del sistema che si vuol esaminare. Tali grandezze sono dette variabili di stato. L'insieme dei loro valori definisce univocamente lo stato del sistema ad un dato istante t, espresso dal vettore a n componenti:
![]()
In molti problemi di Meccanica, lo "stato del sistema" in un dato istante è determinato dall'insieme delle posizioni e delle velocità dei corpi che lo costituiscono. Ad esempio, per un pendolo che oscilla, lo stato ad un certo istante è dato dall'angolo della cordicella rispetto alla verticale e dalla velocità della pallina ad essa appesa. In un ecosistema, lo stato può essere caratterizzato assegnando il numero di individui per ciascuna specie animale che ne fa parte; in un mercato finanziario, i prezzi delle azioni.
Pertanto, a prescindere dalla natura del sistema considerato, il suo stato ad un certo istante viene rappresentato da un vettore x appartenente ad Rn che, com'è noto, può essere pensato come un punto geometrico riferito agli assi di un riferimento cartesiano, in cui le coordinate corrispondono ai valori delle variabili di stato. Così, lo stato di una popolazione di insetti può essere rappresentato in uno spazio unidimensionale (una semiretta, dato che la numerosità della popolazione può assumere solo valori non negativi). Lo stato di un pendolo semplice è rappresentato da un punto in uno spazio bidimensionale (un piano cartesiano) riportando sugli assi il valore dello spostamento angolare rispetto alla verticale e il valore della velocità angolare. Lo stato di un sistema ecologico, in cui sono presenti 4 specie, è rappresentato da un punto in uno spazio a 4 dimensioni. Lo stato di un mercato finanziario è un punto, in uno spazio le cui dimensioni sono tante quanti i titoli trattati. L'insieme di tutti i possibili vettori di stato è detto spazio delle fasi del sistema dinamico.
La variabile t, utilizzata per misurare il tempo che scorre, può essere pensata come un numero reale e allora diremo che il tempo varia in modo continuo, cioè senza salti (come se fosse misurato con un orologio analogico) oppure come un numero naturale, cioè t = 0, 1, 2, ... e diremo allora che il tempo varia in modo discreto, assumendo valori multipli di una data unità di misura, che potrebbe essere un'ora, un giorno o un anno, a seconda del sistema che si sta descrivendo. Nel primo caso si parla di sistemi dinamici a tempo continuo; nel secondo, a tempo discreto.
Quale delle due rappresentazioni sia più adatta a descrivere un sistema reale, dipende dalla situazione che si sta analizzando. Ad esempio, nella descrizione del moto di un pendolo o dello scorrere dei fluidi, si usano sistemi a tempo continuo mentre, nella descrizione dell'andamento temporale di una popolazione di insetti, caratterizzati da stagioni riproduttive, si usano sistemi a tempo discreto con unità di tempo pari all'intervallo che intercorre fra due generazioni successive.
Da un punto di vista formale, conoscere un sistema dinamico significa conoscere una funzione che (una volta assegnato il vettore di stato x0, ad un dato istante iniziale t0) permetta di determinare univocamente lo stato del sistema ad ogni istante di tempo successivo:
![]()
Data una condizione iniziale x0(t0), l'insieme di tutti i valori x(t), ottenuti mediante l'applicazione della funzione F, costituisce la traiettoria del sistema dinamico passante per la condizione iniziale assegnata. In pratica, conoscere le traiettorie significa poter calcolare lo stato del sistema ad un qualunque istante futuro, sulla base della conoscenza dello stato ad un certo istante. In un sistema dinamico a tempo continuo, una traiettoria può essere pensata come una curva nello spazio n-dimensionale delle fasi mentre, in un sistema dinamico a tempo discreto, una traiettoria è costituita da una successione di punti.
In realtà, non è affatto facile conoscere l'operatore F, ma si cerca di risalire ad esso attraverso la formulazione di leggi di evoluzioni locale o equazioni del moto. Nel caso di modelli a tempo continuo, le leggi del moto sono espresse mediante equazioni differenziali, che descrivono come la rapidità di variazione di ciascuna variabile di stato (espressa dalla derivata prima rispetto al tempo) dipenda da se stessa e dalle altre variabili:
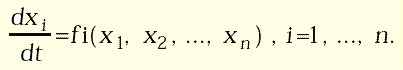
Solo nei casi più semplici si può arrivare ad ottenere la soluzione generale del problema che verifica le condizioni iniziali assegnate, ovvero la funzione F. Ad esempio, consideriamo l'equazione differenziale lineare:

con condizione iniziale x(t0) = x0. La soluzione è:
![]()
In altre parole, partendo da una legge locale, in base alla quale il tasso di variazione di una variabile è proporzionale al valore della variabile stessa, come accade ad esempio nei modelli di crescita di una popolazione (con r > 0) o di decadimento radioattivo (con r < 0), si ottiene in forma esplicita l'operatore di evoluzione temporale che prevede, rispettivamente, una crescita o un decadimento esponenziale.
Un altro esempio famoso è quello di un oscillatore armonico (ad esempio, un corpo appeso a una molla) la cui equazione del moto è espressa dalla seconda legge della dinamica, massa per accelerazione = forza, che diventa un'equazione differenziale del secondo ordine:
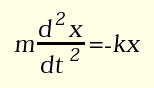
dove la variabile x rappresenta lo spostamento rispetto alla posizione di equilibrio della molla e -kx è la forza elastica di richiamo. Questo modello si presenta in una forma diversa poiché contiene la derivata seconda, ma può essere trasformato introducendo, come seconda variabile di stato, la velocità istantanea

e ottenendo così un sistema di due equazioni differenziali del primo ordine:
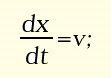
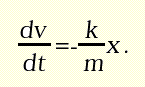
Anche in questo caso è possibile risalire all'espressione analitica della traiettoria: se assumiamo che il corpo parta da fermo, con uno spostamento iniziale x0 rispetto alla posizione di equilibrio, cioè prendiamo come condizione iniziale (x(0), v(0)) = (x0, 0), allora la soluzione è:
![]()

con omega-segnato che è la radice quadrata del rapporto tra k e m. Questa soluzione può essere rappresentata graficamente riportando l'andamento di ciascuna delle due variabili x(t) e v(t) in funzione del tempo (come in Fig.1A) oppure riportando, per ogni t, ivalori di x(t) e v(t) sul piano cartesiano (x,v), come in Fig.1B.
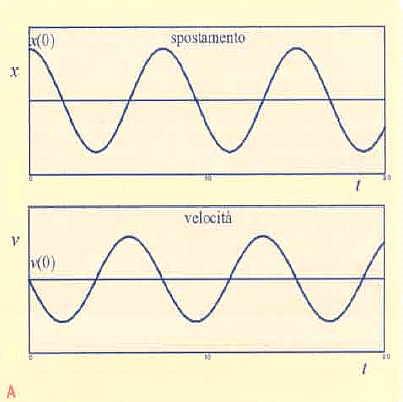
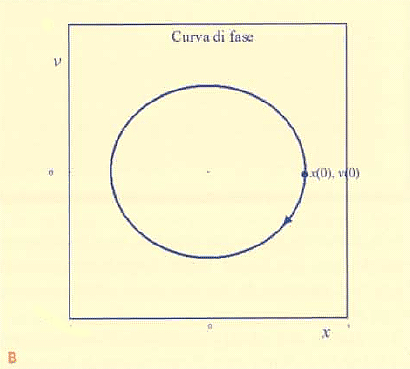
Quest'ultima rappresentazione è detta curva di fase o orbita.
In questi esempi, la facilità ad ottenere le soluzioni in forma analitica è legata al fatto che abbiamo ottenuto equazioni differenziali lineari, in cui cioè i secondi membri erano polinomi di primo grado nelle variabili di stato. Se si considerano modelli non lineari, come spesso accade nella descrizione dei sistemi reali, trovare una soluzione in forma analitica è in genere un'impresa difficile, spesso impossibile.
Analoghe considerazioni valgono anche per modelli dinamici a tempo discreto. In questo caso, preso come unità di misura l'intervallo temporale scelto per scandire il tempo, la legge del moto viene rappresentata sotto forma di equazioni alle differenze:
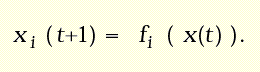
Partendo dalla condizione iniziale, l'intera traiettoria si può ottenere induttivamente: da x(0) si ottiene x(1), il quale può essere preso come nuovo argomento delle funzioni fi per ottenere x(2) e così via, come visualizzato in Fig.2.

Ovviamente, questo procedimento iterativo si basa sull'ipotesi che ciascuna funzione fi abbia come dominio l'insieme M degli stati possibili e che anche i codomini delle fi non escano dallo spazio degli stati, in modo che sia possibile applicare di nuovo le funzioni fi alle variabili di stato. L'esempio più semplice è l'iterazione di una funzione (o mappa) lineare:
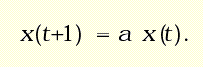
Partendo dalla condizione iniziale x(0), si ottiene:
x(1) = a x(0) ; x(2) = a x(1) = a2 x(0); ...
x(t) = a x(t-1) = a ( a t-1 ) x(0)= a t x(0).
Dalla conoscenza esplicita della successione x(t)= a t x(0), detta progressione geometrica di ragione a, è possibile il calcolo diretto dello stato dopo n intervalli temporali in base alla conoscenza dello stato iniziale. Inoltre, si deduce in modo immediato il comportamento asintotico, per t che tende ad infinito, della traiettoria: per |a|<1, x(t) converge a 0; per |a|>1, x(t) diverge. Inoltre, se è a < 0, l'andamento è di tipo oscillatorio; mentre se a > 0, si ha una successione monotòna.
Ma la situazione non è così semplice, se si considerano leggi del moto non lineari. Infatti, iterando una generica funzione f partendo da una condizione iniziale (o punto seme) x(0), si ottiene:
x(1) = f (x(0)); x(2) = f (x(1)) = f(f(x(0))) = f2 (x(0)); ... ,
x(t) = f (f (x(t-1)) = ft(x(t))
dove ft rappresenta la funzione f composta con se stessa t volte, espressione che in generale sarà estremamente ingombrante e in pratica impossibile da scrivere. Non è facile, quindi, capire il comportamento asintotico delle traiettorie, cioè quale sarà il loro destino al crescere di t.
Con queste premesse formali, siamo ora in grado di dare la seguente definizione: la teoria dei sistemi dinamici è l'insieme dei metodi matematici attraverso i quali si cerca di ottenere, in maniera più o meno esplicita, informazioni sull'operatore di evoluzione temporale F partendo da una sua rappresentazione locale (o legge del moto) assegnata in forma di equazioni differenziali o alle differenze.
Non si tratta di un settore della Matematica particolarmente recente. La sua nascita può essere fatta risalire a Newton, il quale (in una lettera inviata a Leibnitz nel 1677) scrisse che aveva trovato un metodo di lavoro importante, che non poteva rivelare in modo palese. Infatti, lo fece proponendogli un anagramma, in una forma quasi impossibile da decifrare. La frase decodificata, diventata famosa con il nome di anagramma fondamentale del Calcolo, è la seguente:"Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa", che significa: "Data un'equazione che contiene un numero qualunque di quantità fluenti [oggi, diremmo derivate] trovare le flussioni [oggi, diremmo le primitive] e viceversa".
Ovviamente, il metodo divenne poi patrimonio comune e strumento privilegiato per lo studio dei sistemi naturali che evolvono nel tempo, tanto che Pierre Simon de Laplace, nel 1776, ipotizzava l'esistenza di un sistema dinamico in grado di regolare, in modo rigidamente deterministico e prevedibile, l'intero Universo: "lo stato attuale del sistema della natura consegue evidentemente da quello che era all'istante precedente e se noi immaginassimo un'intelligenza che a un istante dato comprendesse tutte le relazioni fra le entità di questo universo, essa potrebbe conoscere le rispettive posizioni, i moti e le disposizioni generali di tutte quelle entità in qualunque istante del futuro".
Laplace sapeva bene che la conoscenza delle diverse entità (quelle che ora chiamiamo variabili di stato) ad un certo istante non può essere ottenuta con infinita precisione, essendo il frutto di processi di misura. Ma, come spesso si assume in base a regole di buon senso, considerava ovvio il fatto che una piccola incertezza nei valori delle condizioni iniziali avesse conseguenze altrettanto piccole sull'intera traiettoria e che quindi il calcolo dello stato futuro risultasse di poco alterato. In altre parole, il fatto di poter rappresentare l'evoluzione di un sistema reale mediante un sistema dinamico, sia pur attraverso una sua rappresentazione locale, era considerato equivalente a dire che la sua evoluzione fosse necessariamente regolare, prevedibile, priva di ogni incertezza.
Eppure, qualche piccolo indizio che le cose non stessero proprio così era già presente in quei settori in cui le equazioni del moto erano non lineari. Ad esempio, nella dinamica dei fluidi, si potevano osservare sia andamenti regolari che complessi. Il fumo di una sigaretta, o il flusso dell'acqua nell'alveo di un fiume, possono talvolta evolvere in modo semplice (il cosiddetto moto laminare) e altre volte in modo vorticoso e disordinato (il cosiddetto moto turbolento) pur essendo governati dalle stesse equazioni del moto. Il passaggio alla turbolenza, che si osserva talvolta in modo improvviso durante il moto di liquidi o gas, è stato uno dei problemi che maggiormente hanno stimolato gli studi sui sistemi dinamici non lineari. Si racconta che Heisenberg, uno dei padri della Fisica quantistica e premio Nobel per la Fisica nel 1932, pochi minuti prima di morire abbia detto: "quando nell'aldilà avrò l'opportunità di interrogare il Creatore, gli voglio chiedere due cose: perché la relatività e perché la turbolenza. Almeno sulla prima spero di ottenere una risposta".
In effetti, agli inizi del XX secolo l'interesse per questo settore sembrava destinato a ridursi, per mancanza di argomenti nuovi da proporre. C'erano problemi non risolti, come la turbolenza dei fluidi, ma la loro soluzione appariva così difficile e lontana che sembrava non valesse la pena dedicarvi ulteriori sforzi.
I motivi per il risveglio di interesse vennero dagli studi del matematico, fisico e filosofo francese Henri Poincaré (1854-1912) che può essere considerato il fondatore della teoria qualitativa (o topologica) dei sistemi dinamici ovvero di un modo di studiare le leggi del moto che rinuncia a ogni pretesa di conoscenza analitica o numerica delle soluzioni e si basa su metodi di tipo geometrico-visivo. Partendo da un problema apparentemente semplice, il moto di tre corpi che interagiscono tra loro attraverso la forza di gravità, Poincaré arrivò a descrivere in modo chiaro il fenomeno del caos deterministico, scrivendo nel 1903: "una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora diciamo che l'effetto è dovuto al caso. Se conoscessimo esattamente le leggi della natura e la situazione dell'universo all'istante iniziale, potremmo prevedere esattamente la situazione dello stesso universo in un istante successivo. Ma se pure accadesse che le leggi naturali non avessero più alcun segreto per noi, anche in tal caso potremmo conoscere la situazione iniziale solo approssimativamente. Se questo ci permettesse di prevedere la situazione successiva con la stessa approssimazione, non ci occorrerebbe di più e dovremmo dire che il fenomeno è stato previsto. Ma non è sempre così; può accadere che piccole differenze nelle condizioni iniziali ne producano di grandissime nei fenomeni finali. Un piccolo errore nelle prime produce un errore enorme nei secondi. La previsione diviene impossibile".
In effetti, la visione di Laplace (oltre che nei sistemi lineari) è corretta anche nei sistemi non lineari, purché lontani dai regimi di comportamento caotico. Ma in modelli non lineari, anche semplici, le traiettorie possono risultare molto simili a successioni di stati aleatori, cioè ottenuti con l'intervento di elementi casuali (come le uscite nel lancio di un dado).
I risultati ottenuti da Poincaré erano probabilmente troppo avanzati rispetto ai suoi tempi e non suscitarono subito l'interesse che meritavano. Ma la rivoluzione scientifica provocata dalla scoperta del caos deterministico era solo ritardata. Dopo ulteriori importanti contributi alla teoria qualitativa dei sistemi dinamici, forniti dalla grande scuola russa dagli anni '30, con Lyapunov, Kolmogorov, Andronov, Pontrjaguine e dagli studi di Birkhoff negli Stati Uniti, due articoli diedero un decisivo contributo alla diffusione e alla crescente popolarità di questo settore della Matematica: quello del 1963 del meteorologo americano Edward Lorenz e quello del 1976, dal titolo Semplici modelli matematici con dinamiche molto complicate, in cui Robert May - un fisico inglese che studia modelli per l'Ecologia - illustrò con un linguaggio accessibile anche a non specialisti l'insorgere di dinamiche caotiche attraverso lo studio di un sistema dinamico a tempo discreto, ottenuto iterando un polinomio di secondo grado (una "banale" parabola).
Seguiamo anche noi la strada indicata da May, analizzando il seguente modello dinamico a tempo discreto:
x (t+1) = f (x(t))= (1 - r - sx(t)) x(t) - h.
Questa equazione alle differenze ci permette di introdurre alcuni importanti concetti che caratterizzano anche i sistemi dinamici non lineari a tempo continuo. Essa costituisce anche un modello per descrivere l'andamento temporale di una popolazione di densità x dove il parametro r rappresenta il tasso di crescita nell'unità di tempo, il termine -sx rappresenta un termine di mortalità dovuta a sovraffollamento (competizione per il cibo o per lo spazio vitale) e -h il tasso di prelievo (ad esempio, se parliamo di popolazioni ittiche, un'attività di pesca a quote fisse).
Il primo passo per affrontare lo studio qualitativo di un sistema dinamico consiste nell'identificarne i punti di equilibrio (o stati stazionari) definiti come quei valori della variabile di stato che rimangono costanti sotto l'azione della legge del moto: x(t+1) = x(t). Si tratta quindi dei punti fissi della funzione f, soluzioni dell'equazione f(x)=x, rappresentati graficamente dalle intersezioni del grafico della funzione y = f(x) con la retta bisettrice di equazione y = x. Nel caso del nostro modello, è f (x) = -sx2 + (1-r) x -h e quindi l'equazione f(x) =x dà sx2 + rx + h = O. Per h < r2/(4s) si ottengono allora due punti fissi:


Se la condizione iniziale viene presa in corrispondenza di un punto fisso x*, la traiettoria che si ottiene è stazionaria, cioè x(t) = x* per ogni t.
È allora naturale chiedersi cosa succede se, anziché partire esattamente da x*, si parte da una condizione iniziale x(0) vicina a x*. Per analizzare questo problema, ricorriamo a una comoda costruzione grafica per studiare le traiettorie ottenute dall'iterazione di una funzione di una sola variabile.
Consideriamo il grafico della funzione y = f (x), che nel nostro esempio è una parabola concava, e sovrapponiamo ad esso il grafico della bisettrice y = x. Partendo dalla condizione iniziale x(0), presa sull'asse delle ascisse, tracciamo un segmento verticale fino a incontrare il grafico della funzione e poi procediamo in orizzontale fino all'asse y per ottenere x (1) = f (x(0)). Per procedere nell'iterazione, occorre ora riportare x(1) sull'asse delle ascisse, in quanto dovrà diventare il nuovo argomento su cui applicare la funzione per ottenere x(2). Questo può essere ottenuto sfruttando la presenza della bisettrice che, essendo il luogo di equazione y = x, permette di riportare x(1) sull'asse orizzontale mediante uno spostamento orizzontale verso destra e uno verticale verso il basso, usando la bisettrice come punto di svolta. Ora siamo pronti a ripetere lo stesso procedimento per ottenere x(2) = f (x(1)) e così via. Si può notare l'inutilità del segmento che congiunge il grafico della funzione con l'asse delle y (che viene subito ripercorso all'indietro verso la bisettrice) e lo stesso ragionamento si può applicare al segmento verticale: per non percorrerlo due volte, prima in discesa e poi in salita, è conveniente fermarsi sulla bisettrice e da qui subito dirigersi verso il grafico per determinare l'iterato successivo. In tal modo, la sequenza di passi da un iterato al successivo diventa: x(t) (sulla bisettrice) -> tratto verticale ->grafico della funzione -> tratto orizzontale -> x(t+1) (sulla bisettrice) come visualizzato in Fig. 3. Si viene così a sostituire l'asse x con la bisettrice ed è su essa che si rappresenta la sequenza {x(0),
x(1), ..., x(t), ...}.
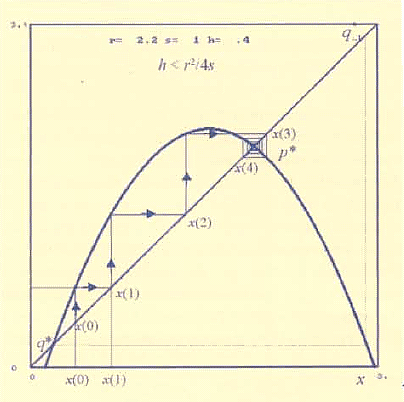
Figura 3
Dalla Fig. 3 (ottenuta con parametri r = 1.5, s = 1, h = 0.2) ci rendiamo conto che i due equilibri si comportano diversamente. Partendo da una condizione iniziale in un intorno di q*, la traiettoria si allontana da esso (e non vi ritorna più); partendo da una condizione iniziale vicina a p*, la traiettoria generata si avvicina invece asintoticamente ad esso cioè converge a p*. Si dice allora che q* è un equilibrio instabile (o repulsivo) mentre p* è asintoticamente stabile (o attrattivo).
La differenza fra i due equilibri si può giustificare osservando la pendenza con cui il grafico della funzione attraversa la bisettrice in corrispondenza dei punti fissi: in q* la pendenza è superiore a quella della bisettrice, cioè il coefficiente angolare f ´(q*) della retta tangente al grafico, x(t+1) = q*+ f ´(q*) (x(t)-q*), è maggiore di 1. Quindi la funzione iterata si comporta, in un intorno del punto fisso, come una mappa lineare di ragione maggiore di 1 (una progressione geometrica espansiva). Applicando lo stesso ragionamento all'equilibrio p*, possiamo invece dire che l'approssimazione lineare della funzione in un suo intorno si comporta come una progressione geometrica contrattiva, essendo il coefficiente angolare della tangente minore di 1 in valore assoluto. Inoltre, la convergenza è di tipo oscillatorio (con oscillazioni smorzate) in quanto il coefficiente angolare in p* è negativo.
La stabilità è un concetto locale, poiché viene definita in base al comportamento delle traiettorie che partono da condizioni iniziali prese vicino all'equilibrio. La domanda che sorge spontanea - quanto vicine? - porta al concetto di bacino di attrazione, definito come l'insieme dei punti che generano traiettorie convergenti a un dato attrattore. Nel nostro caso, il bacino è delimitato dal punto fisso instabile e dalla sua pre-immagine, indicata con q*-1 in Fig. 3 (pre-immagine di q* significa che f (q*-1) = q*). Nella situazione di Fig. 3, si hanno quindi due tipi di dinamiche asintotiche: se x(0)‘ (q*,q*-1), allora la traiettoria che parte da x(0) converge all'equilibrio p*; per x(0) < q* oppure x(0) > q*-1, la traiettoria diverge invece a -infinito (per l'applicazione considerata, questo equivale all'estinzione della popolazione).
Entrambi i valori di equilibrio dipendono dal parametro h e al crescere di h si avvicinano tra loro: p* diminuisce e q* aumenta (aumentando la quota prelevata nell'unità di tempo, il valore di equilibrio stabile diminuisce e il valore di soglia, sotto il quale la specie andrà all'estinzione, aumenta ovvero il sistema diventa più vulnerabile).
Quando il parametro h raggiunge il valore h = r2/4s, i due punti di equilibrio si sovrappongono e la parabola diventa in tali punti tangente alla bisettrice (Fig. 4A). Un ulteriore aumento di h provoca la scomparsa dei due equilibri, dopo di che l'unica evoluzione possibile è quella che conduce all'estinzione (Fig. 4B).
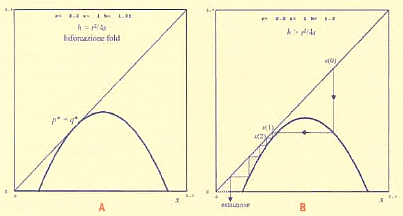
Figura 4
Il valore h = r2/4s è un valore di biforcazione, che prende il nome di biforcazione tangente (o biforcazione fold). In generale, si dice che un parametro attraversa un valore di biforcazione quando determina il passaggio fra due situazioni dinamiche qualitativamente diverse, dovuto ad esempio alla creazione o scomparsa di punti fissi o altri tipi di attrattori, oppure cambiamenti di stabilità.
Nell'esempio proposto, le biforcazioni che portano al caos si verificano agendo sui parametri in modo da rendere più acuminata la parabola. Per mostrare ciò, fissiamo h = 0 (popolazione non sfruttata) e facciamo aumentare il parametro r, usandolo come una "manopola" per innalzare il vertice. Per h=0, i punti fissi diventano q*=0 e p*= r/s (valore di equilibrio della popolazione non sfruttata). Al crescere di r, il grafico della funzione in corrispondenza del punto fisso p* diventa via via più ripido, fino a che la pendenza raggiunge il valore -1, cioè la tangente diventa perpendicolare alla bisettrice. Questo accade per r = 2, poiché il coefficiente della retta tangente al grafico in p* è f ´(p*) = 1+r - 2sp*= 1-r. Un aumento ulteriore di r provoca quindi una perdita di stabilità dell'equilibrio positivo; r = 2 costituisce pertanto un valore di biforcazione. Per cercare di capire il tipo di biforcazione, esaminiamo il comportamento dinamico delle traiettorie per valori di r poco maggiori di 2 e con condizione iniziale prossima a p*. Quello che si può vedere è che la traiettoria si allontana da p*, oscillando, e tende a un'oscillazione periodica fra due punti (indicati con alfa e beta in Fig. 5A).
Partendo da uno di questi due punti, si ottiene una traiettoria che saltella tra alfa e beta, essendo f(alfa) = beta e f(beta) = alfa. Inoltre, allo stesso ciclo-2 tende ogni traiettoria che parte da una condizione iniziale x(0)‘ (q*,q*-1) = (0, (1+r)/s), esclusa x(0) = p* naturalmente. Questo tipo di biforcazione si chiama biforcazione con raddoppio del periodo o, più brevemente, biforcazione flip.
Per capire meglio quello che accade, consideriamo la funzione composta F(x) = f (f (x))=
f 2(x), il cui grafico è mostrato in Fig. 5B. Poiché F(x) è un polinomio di quarto grado, può avere fino a 4 intersezioni con la bisettrice, ossia quattro punti fissi. Due sono necessariamente gli stessi di f, ossia q* e p*, mentre eventuali altri corrispondono ai punti periodici (di periodo 2) di f essendo F(alfa) =
f (f (alfa)) = f(beta) =alfa e, analogamente, F(beta)=beta. In effetti, iterare la mappa F significa generare gli stati del sistema a salti di 2.
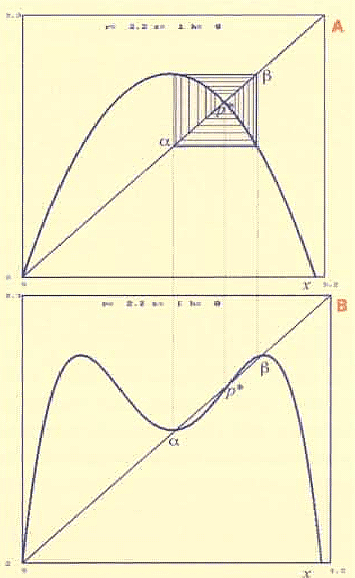
Figura 5
La biforcazione che avviene nella mappa f per r=2 corrisponde a ua perdita di stabilità di p* anche per l'iterata: è F ´(p*)=[f ´(p*)]2 e quindi abbiamo F ´(p*) „ 1 per r „ 2. Aumentando ulteriormente il parametro r, anche la pendenza di F nei suoi punti fissi alfa e beta raggiunge il valore -1 e quindi avviene una biforcazione flip che fa diventare alfa e beta instabili per F, mentre attorno a ciascuno di loro si crea un ciclo di F di periodo 2. Tali cicli-2 stabili rappresentano un ciclo-4 stabile per f, che diventa l'attrattore "di turno" del sistema dinamico, e contemporaneamente costituiscono 4 punti fissi stabili per f4. Aumentando ancora r, tale ciclo-4 diventerà instabile lasciando il posto a un ciclo-8 così via. È naturale chiedersi cosa avverrà nel seguito: si raggiungerà un ciclo di periodo massimo (dopo il quale, le biforcazioni con raddoppio del periodo finiranno) o i raddoppi continueranno all'infinito?
Per analizzare ciò, si ricorre alla costruzione di un diagramma di biforcazione. Si considera un piano cartesiano in cui si riportano sull'asse orizzontale i valori del parametro r preso in un certo intervallo, ad esempio r appartente all'intervallo [1,3] e per ogni valore del parametro si calcolano i primi N punti della traiettoria, dove N è un numero sufficientemente grande (ad esempio N = 500). Sulla verticale passante per il valore di r utilizzato, si riportano i valori "asintotici" della x, cioè i valori più avanzati fra quelli calcolati, ad esempio i valori {x201, ...,x500}. Infatti, una volta eliminato il transitorio {x0, ...,x200}, i valori rappresentati si troveranno sull'attrattore "di turno" e quindi la loro posizione può essere considerata come una rappresentazione dell'attrattore per il valore del parametro considerato.
In Fig. 6 (seguendo il diagramma di biforcazione) possiamo osservare che, al crescere di r, si hanno successivi raddoppi di periodo: da 4 a 8, poi a 16, 32, ... e tutta la successione delle potenze di 2.
Inoltre è importante osservare che i valori di r, per i quali avvengono le biforcazioni di raddoppio del periodo, da 2k a 2k+1, sono sempre più vicini fra loro al crescere di k. Infatti, la variazione di r necessaria per passare dalla creazione del ciclo-2 (che avviene per r = r1= 2) alla creazione del ciclo-4, che avviene per r = r2= EF6, è di (Delta(r))1=
(r2- r1) (circa) = 0.449 , mentre la variazione di r che intercorre fra la creazione del ciclo-4 e del ciclo-8 è (Delta(r))2=(r3 - r2) (circa) =
(3.544-3.449) = 0.095. I raddoppi di periodo diventano sempre più frequenti, ovvero gli intervalli (Delta(r))k diventano sempre più piccoli. Ciò si può osservare nel diagramma di biforcazione di Fig. 6, in cui è evidente che il ciclo attrattivo di turno rimane tale per un intervallino dell'asse delle ascisse sempre più piccolo.
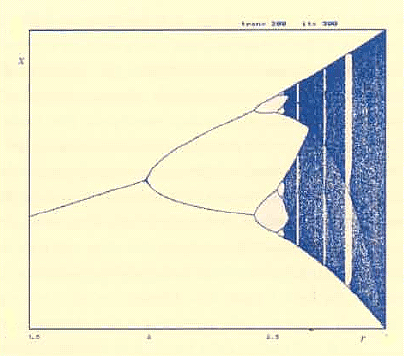
Figura 6
In realtà, per r > 2.56 si ha una sequenza di valori di biforcazione così numerosi e ravvicinati da far pensare appunto ad una cascata. La cosa più sorprendente è che, per valori di r vicini a 2.57, gli infiniti cicli di periodo 2k, k appartenente ad N, sono stati tutti creati. In altre parole, la sequenza di valori di biforcazione {r1, r2, ..., rn, ...} ha un punto di accumulazione, noto come numero di Feigenbaum, e dato da rinfinito=2.56994...
Dopo questo valore di r compaiono delle traiettorie che non sono periodiche. Sono cioè costituite da valori che non coincidono mai con un valore già ottenuto, caratterizzate dal fatto che i punti riempiono densamente uno o più intervalli. Infatti, nel diagramma di biforcazione cominciano a comparire, lungo la verticale, delle zone nere (densamente riempite di punti). Se prendiamo una di tali traiettorie e la rappresentiamo lungo l'asse dei tempi, otteniamo sequenze di punti come quelle mostrate in Fig. 7A, ottenuta per r = 2.678. Da questi andamenti, si intuisce l'origine del termine caos deterministico: sebbene i valori delle x(t) siano ottenuti attraverso l'applicazione ripetuta della funzione f - un meccanismo puramente deterministico - questi sembrano susseguirsi in modo apparentemente casuale, senza alcuna regolarità o ricorrenza.
Una delle cause di un comportamento così disordinato è da ricercarsi nel fatto che, intrappolati all'interno dell'intervallo in cui si muovono le traiettorie caotiche, ci sono infiniti punti periodici repulsivi. Essendo le traiettorie limitate, poiché i valori ottenuti iterando la mappa non possono uscire dall'intervallo I = (0, r/4), e non convergendo ad alcun ciclo attrattivo, esse "rimbalzano" continuamente, respinte dai punti periodici repulsivi che sono sparsi (e densi) all'interno dell'intervallo I.

Figura 7
Un altro fatto importante, e per molti aspetti stupefacente, caratterizza le traiettorie caotiche: la difficoltà di ottenerne due identiche. In linea di principio, data la stessa mappa e data la stessa condizione iniziale, le traiettorie dovrebbero essere identiche. Ma quando le traiettorie sono caotiche, basta una minima differenza fra due condizioni iniziali per ottenere traiettorie completamente diverse. E minime differenze possono anche essere introdotte a causa della precisione limitata con cui vengono rappresentati i numeri ovvero dal numero delle cifre usate per fare i calcoli.

Questo fatto è illustrato in Fig. 7B, dove la prima traiettoria è stata ottenuta partendo da una certa condizione iniziale mentre la seconda è stata ottenuta con una condizione iniziale, che differisce di pochissimo, solo un milionesimo ovvero 10-6 = 0.000001. Ebbene, dopo alcune iterazioni in cui si ottengono valori simili, le due traiettorie cominciano a differenziarsi sempre di più, fino a diventare completamente diverse. Il fatto che una piccola variazione nelle condizioni iniziali (anche quasi impercettibile o difficilmente misurabile) abbia conseguenze così notevoli nell'evoluzione di un sistema dinamico caotico è stato chiamato sensitività rispetto alle condizioni iniziali o anche effetto farfalla.
Cos'è quindi il caos deterministico? In realtà, una sua definizione generale, applicabile a tutti i casi in cui tale fenomeno si manifesta, non esiste ancora. Si riconosce la presenza del caos in tutti i casi in cui si ottengono traiettorie limitate che soddisfano le seguenti tre condizioni:
(1) Sensitività rispetto alle condizioni iniziali: partendo da due diverse condizioni iniziali, arbitrariamente vicine fra loro, la distanza fra le rispettive traiettorie cresce esponenzialmente e, dopo un numero finito di iterazioni, diventa dello stesso ordine di grandezza della variabile di stato.
(2) Transitività (o mixing): i punti della traiettoria generata, partendo da una generica condizione iniziale, ricoprono densamente una zona dello spazio delle fasi.
(3) Esistenza di infiniti cicli repulsivi, con i punti periodici densi nella regione ricoperta dalle traiettorie caotiche.
Si può dimostrare che le proprietà (2) e (3) implicano la (1), ma la proprietà di sensitività alle condizioni iniziali viene in genere riportata in quanto è quella più semplice ed evidente (ed è anche la più famosa).
Per capire le caratteristiche geometriche, o topologiche, del caos deterministico, si deve tenere presente che la mappa considerata (la parabola) agisce su un segmento allungandolo in certe zone e comprimendolo in altre. Se il segmento include il punto critico x=1/2, lo ripiega anche (si veda Fig. 8A). Alla seconda applicazione della f, tali azioni si ripetono (si veda Fig. 8B) e così via. L'iterazione della funzione equivale quindi all'applicazione di ripetute azioni di stiramento, piegamento, compressione.
L'azione combinata di queste azioni è possibile solo con mappe non lineari, in quanto una mappa lineare o dilata o contrae (ma non entrambe le cose contemporaneamente) e non può certo causare piegamenti.
L'insorgere del caos deterministico è invece legato alle trasformazioni che provocano stiramenti e ripiegamenti. Spesso viene usata la metafora dell'azione geometrica che si esercita sull'impasto di farina e acqua quando, con il noto procedimento casalingo, si prepara la sfoglia. La principale caratteristica geometrica delle trasformazioni che generano successioni caotiche consiste in azioni combinate (e ripetute durante l'iterazione) di stiramento e ripiegamento (stretching & folding).
Il significato geometrico delle proprietà (1) e (2) risulta meglio comprensibile proprio attraverso la metafora della sfoglia. Iterando tante volte il processo di allungamento (stretching) e ripiegamento (folding), due particelle di impasto, che si trovano vicine ad un certo istante, verranno a trovarsi lontane dopo un numero finito di iterazioni (proprietà 1); un pizzico di farina inizialmente concentrato in un punto finirà con il trovarsi uniformemente distribuito su tutto l'impasto (proprietà 2).
Anche per la proprietà (3) possiamo fornire una semplice giustificazione intuitiva. Se le traiettorie di un sistema dinamico sono limitate, ovvero sono costrette a rimanere intrappolate in una regione compatta dello spazio delle fasi e tale regione è densamente ricoperta di punti periodici repulsivi, allora le traiettorie non possono che essere estremamente irregolari, come il moto di una particella che si muove in uno spazio densamente riempito di altre particelle che la respingono.
Il concetto di Caos ha sempre avuto una connotazione prevalentemente negativa essendo il più delle volte contrapposto al concetto di ordine. Malgrado ciò, il caos ha sempre rappresentato qualcosa di affascinante per molti poeti ed artisti che vedevano in questa immagine evocativa non soltanto la degenerazione dell'ordine, ma anche quel contesto denso di potenzialità da cui può emergere la forma, la creazione.
Forse fu proprio questo fascino ambiguo a spingere alcuni scienziati [Yorke, 1972] a definire Chaos una serie di idee che apparentemente contraddicono l'accezione corrente. Da allora questa teoria ha profondamente influenzato gli ambienti scientifici e culturali e sta producendo, si potrebbe dire, una rivoluzione in alcuni paradigmi di pensiero. In questo articolo di carattere introduttivo ci proponiamo di illustrare alcuni concetti fondamentali quali attrattori caotici ed auto-organizzazione, cercando, attraverso degli esempi intuitivi, di evidenziare il carattere di interdisciplinarietà e l'impatto culturale e tecnologico che queste teorie stanno promuovendo in molti campi della conoscenza.
Senza volere evidentemente esaurire in questo breve articolo tutto l’argomento e i diversi interessi culturali che ad esso fanno riferimento, in alcuni riquadri si daranno dei cenni storici sui percorsi di sviluppo delle conoscenze fisiche avutisi sui sistemi dinamici (riquadro 1) e sui sistemi complessi (riquadro 2)...
Caos Deterministico e cambiamento di paradigma
Il termine Caos Deterministico, in campo scientifico, fu riferito ad alcuni sistemi dinamici non lineari (sistemi caotici) che pur essendo impredicibili e apparentemente incomprensibili per la loro complessità, nascondono un ordine interno che può essere rivelato con un approccio molto diverso da quello utilizzato nella scienza lineare.
Il primo paradosso è che i sistemi caotici sono in realtà ordinati pur essendo impredicibili. Essi possono essere considerati una ampia fascia di sistemi situati tra i sistemi lineari ed i sistemi randomici (mancanza totale di correlazione tra due campioni successivi). Il secondo paradosso fu l’uso dell’aggettivo Deterministico per sottolineare il fatto che la mancanza di predicibilità di questi sistemi non è dovuta a forze o rumori esterni al sistema, ma dipende da una caratteristica intrinseca del sistema stesso: la elevata sensibilità alle condizioni iniziali.
Questa definizione fondamentale, significa che nei sistemi caotici, cambiando anche di poco le condizioni iniziali, la evoluzione della dinamica del sistema cambia notevolmente nel tempo. Poiché le condizioni iniziali non possono, in pratica, essere conosciute con precisione infinita, questo significa che anche possedendo un modello esatto del sistema (i.e.: tutte le equazioni che descrivono il sistema), nella grande maggioranza dei casi non sia possibile prevedere la evoluzione di un sistema per un tempo lungo. In alcuni semplici sistemi caotici [mappa di Bernouilli] si può addirittura mostrare che la memoria delle condizioni iniziali viene inesonerabilmente persa nel tempo.
In poche parole il futuro non è determinato o determinabile; le equazioni della dinamica dei sistemi caotici non sono sufficienti a descrivere completamente i fenomeni; il caos nasconde strutture ordinate; il determinismo non significa di per sé predicibilità.
Attrattore ed ordine
Il secondo tassello del mosaico del Caos è costituito dalla nozione di attrattore. Questo termine rappresenta un concetto molto importante per capire il tipo di ordine dei sistemi caotici.
Per definire l'attrattore si ricorre ad uno spazio di stato in cui sono rappresentate le variabili dinamiche del sistema. Per alcune considerazioni che verranno illustrate successivamente, si utilizza lo spazio delle fasi in cui sono rappresentati i valori di una grandezza e delle sue derivate rispetto al tempo. Il numero di dimensioni dello spazio delle fasi dipende dal numero di equazioni differenziali che modellizzano il sistema. Nello spazio delle fasi la variabile temporale è implicita e la dinamica dei sistemi regolari può essere rappresentata da punti fissi o cicli limite (percorso costante nel tempo). I sistemi caotici presentano invece fasci di traiettorie. Poiché ogni punto dello spazio rappresenta una funzione di stato del sistema, due traiettorie diverse non possono avere punti in comune (altrimenti dovrebbero coincidere). In fig. 1 abbiamo riportato uno degli attrattori più noti : l’attrattore di Lorenz [Lorenz, 1963].

Fig. 1: Attrattore di Lorenz: ogni traiettoria dell'attrattore è in realtà composta da due traiettorie molto vicine che divergono nella evoluzione dinamica del sistema.
Le traiettorie che hanno punti molto vicini (condizioni iniziali molto simili) divergono nel tempo formando un intreccio molto articolato. Malgrado questo potrebbe far pensare ad un sistema del tutto casuale ed impredicibile, i fasci di traiettorie nello spazio delle fasi mostrano delle strutture organizzate. é come se le linee che rappresentano la dinamica del sistema si conformassero ad un ordine superiore definito dal luogo dei punti dello spazio visitati dal sistema cui è stato dato il nome di attrattore. Il termine sta ad indicare che il sistema tende (viene attratto) verso un modello di comportamento dinamico senza però ripetersi in modoidentico.
[...]
Auto-organizzazione, struttura e sistemi
[...]
L’Auto-Organizzazione è la proprietà manifestata da alcuni sistemi complessi formati da molteplici elementi che interagiscono tra loro, di sviluppare strutture ordinate da situazioni caotiche. Questi sistemi sono capaci di creare organizzazione e strutturazione facendo crescere la complessità interna anche quando i singoli elementi del sistema si muovano in modo autonomo ed in base a regole puramente locali. Secondo un definizione data da Klir [Klir, 1991]: "un sistema auto-organizzante è un sistema che tende a migliorare le sue capacità nel corso del tempo organizzando meglio i suoi elementi per raggiungere l'obiettivo". Essi sono sistemi (orientati all’obiettivo) capaci di migliorare le loro prestazioni, senza un aiuto esterno, mentre stanno tendendo verso l'obiettivo.
Poiché la definizione dell'obiettivo è funzione delle proprietà comportamentali che si vogliono osservare, la definizione non è univoca ma piuttosto qualitativa. Generalmente per comportamento auto-organizzante si intende la formazione spontanea di strutture e patterns indipendentemente dalle condizioni iniziali. Malgrado siano sistemi dinamici con elevato numero di elementi e variabili, quindi con uno spazio di stato molto ampio, essi tendono a concentrare il proprio attrattore in una porzione limitata dello spazio.
Tra i sistemi auto-organizzanti, una classe a parte sono quei sistemi che hanno al loro interno meccanismi genetici che mettono in atto un altro principio di adattamento: quella della selezione naturale. Queste caratteristiche, tipiche dei sistemi formati da individui viventi, conferiscono al sistema una dimensione in più esaltando la strutturazione della complessità interna nella direzione dell’adattamento.
[...]
Il Caos Deterministico
Le prime intuizioni sui sistemi caotici risalgono agli anni 1910-1930. Gli studi effettuati da H. Poincarè, G.D. Birkhoff e S. Smale evidenziarono come alcuni sistemi fisici non lineari mostrano traiettorie evolutive molto complesse la cui dinamica dipende fortemente dalle condizioni iniziali. In quegli anni la tecnologia (calcolatori elettronici) non era matura per permettere un approfondimento delle intuizioni iniziali e probabilmente la concomitanza con altre scoperte importanti (la relatività e la teoria quantistica) contribuirono a limitare lo sviluppo di questa linea di pensiero fino agli anni '60.
Attrattori e frattali
Più tardi, furono proprio le simulazioni al computer di E. Lorenz [Lorenz, 1962] a mettere in risalto come un semplice sistema di tre equazioni differenziali non lineari mostri chiaramente la dipendenza dalle condizioni iniziali. Diverse simulazioni, condotte su un modello della circolazione atmosferica, pur partendo dalle medesime condizioni iniziali mostravano una divergenza che si amplificava nel tempo. Inoltre, i tempi in cui si verificava la divergenza erano più lontani se si aumentava la precisione (in bit) utilizzata per la simulazione stessa. In sostanza per quanto fosse piccola la differenza tra le condizioni iniziali, queste si amplificavano nel tempo risultando in una impredicibilità del sistema.
Osservando le traiettorie nello spazio delle fasi (fig. 1), Lorenz notò che aumentando la risoluzione con cui si osserva il sistema ogni traiettoria si sdoppia in due linee quasi coincidenti per un certo tratto. Egli mise in relazione questa caratteristica con un altro settore di ricerca che si sviluppò negli anni 70: la geometria frattale di cui più avanti daremo dei cenni. Dimostrò infatti che il suo attrattore aveva una dimensione non intera ma frazionaria (2.06). Per questo motivo chiamò il suo attrattore strange attractor, termine che viene attualmente utilizzato per indicare attrattori con dimensione frazionaria.
La geometria frattale fu introdotta da B. Mandelbrot negli anni '70 [Mandelbrot, 1983] con lo scopo di dare una descrizione formale della complessità delle forme naturali. Essa parte da una proprietà che si manifesta molto spesso nelle forme naturali: l'autosomiglianza, ossia la somiglianza tra le parti ed il tutto. Nel tentativo di descrivere una invariante che caratterizzasse l'autosomiglianza, Mandelbrot approdò alla ridefinizione del concetto di misura. L'esempio provocatorio (e ormai famoso) che egli propose per spiegare questa necessità fu quello della misura della lunghezza della costa della Gran Bretagna. Egli mostrò che la misura cambiava in funzione della lunghezza dello strumento utilizzato per la misura (righello). é abbastanza evidente che utilizzando righelli da dieci chilometri, da un metro, o da un micron per ottenere questa misura otterremo risultati dipendenti dalla unità utilizzata.
Mandelbrot individuò una relazione tra queste misure apparentemente casuali facendo ricorso ad una grandezza introdotta da Hausdorff nel 1919. Egli notò che il rapporto tra il logaritmo del risultato della misura (numero N delle unità di misura) ed il logaritmo dell'inverso del valore della unità di misura (r) assume un valore costante (D).
D = log(N) / log(1/r)
La variabile D rappresenta il grado di frastagliatura di una linea e poiché in natura assume sempre dimensioni frazionarie, fu chiamata da Mandelbrot dimensione frattale.
L'importanza degli studi di Lorenz fu quella di stabilire un collegamento tra la descrizione frattale e gli attrattori introducendo cosi una delle più interessanti invarianti della dinamica (la dimensione frattale) che caratterizza la evoluzione temporale di un sistema.
Biforcazioni ed analisi dinamica dei sistemi caotici
Successivamente alle prime idee di Lorenz e Mandelbrot la teoria del caos si è articolata in una serie di studi e di branche ed ha costituito l'ossatura della maggior parte delle indagini sulla dinamica dei sistemi. Già negli anni '60 e successivamente negli anni '70 il matematico francese René Thom [Thom, 1975] con la Teoria delle Catastrofi anticipò quello che sarebbe stato uno dei principali approcci degli anni successivi. Le catastrofi furono definite come momenti di passaggio (successivamente indicate come biforcazioni tra differenti stati di equilibrio in relazione a variazioni anche piccole di parametri di controllo del sistema. Thom studiò e classsificò le modalità sotto cui questi eventi avvengono, in relazione a quanti parametri vengono contemporaneamente cambiati.
Una delle prime applicazioni modellistiche dell'analisi dei sistemi caotici di notevole rilevanza fu la revisione dell'approccio classico alla turbolenza da parte di Ruelle e Takens [Ruelle, Takens, 1971]. Essi ipotizzarono che la turbolenza fosse il risultato di un particolare regime dell'attrattore nelle equazione di Navier Stokes. Fu mostrato che il raggiungimento del regime turbolento avveniva attraverso il passaggio di una serie di Biforcazioni di Hopf, ossia il passaggio nell'attrattore da un punto fisso ad un orbita periodica, successivamente ad un orbita pseudoperiodica toroidale ed infine ad un attrattore strano [Ruelle, 1987]. Infine essi confermarono questa teoria attraverso una serie di esperimenti con fluidi reali.
Il concetto di biforcazione come un cambiamento qualitativo nella struttura dell'attrattore, è stato ampiamente ripreso e studiato negli anni successivi; poiché le modalità di biforcazione sono in numero limitato, esse costituiscono la base per molti studi di modellistica il cui scopo principale è quello di scoprire quali sono i meccanismi che inducono il caos in un sistema e risalire quindi alle caratteristiche del modello stesso. Questa branca di ricerca viene identificata come qualitative dynamics e mette l'accento sulla caratteristica multidisciplinare della teoria del caos in quanto ricerche sulle fenomenologie comuni a molti sistemi. Uno degli esempi più noti è il meccanismo di progressione caotica del period doubling che dà luogo a straordinarie somiglianze di comportamento tra fenomeni molto diversi tra loro e consiste nel progressivo raddoppio del numero degli stati assunti dal sistema allorché un parametro esterno viene variato.
L'analisi dei sistemi caotici reali
A partire dagli anni '80, sono stati sviluppati una serie di concetti che hanno creato un legame tra la Teorie del Caos Deterministico e le applicazioni in campo industriale ed oggi costituiscono il nodo tra la scienza e la tecnologia dei sistemi caotici. In particolare questi studi focalizzano la loro attenzione sull'analisi di segnali provenienti da sensori installati su sistemi caotici o presunti tali. Le principali applicazioni riguardano lo sviluppo di modelli, la classificazione, la predizione, il controllo e la sincronizzazione dei sistemi caotici. Questi sistemi spesso presentano un grado di complessità notevole sia per la mancanza di adeguati modelli teorici e sia a causa della presenza di rumore nei segnali dovuti a fenomenologie concomitanti che mascherano parzialmente la dinamica causando un aumento artificiale della dimensionalità.
Malgrado gli studi sui sistemi caotici furono intrapresi negli anni '60-'70, soltanto all'inizio degli anni '80 [Takens, 1981] furono applicate tecniche di ricostruzione degli attrattori relativi a segnali di sistemi reali. Le difficoltà nella ricostruzione dello spazio delle fasi sono insite nel fatto che generalmente si dispone di una sola o di poche variabili che governano il sistema e quindi non era chiaro come si potesse passare da osservazioni univariate alla dinamica multivariata.
A dare soluzione a questi problemi e ad aprire la strada alle applicazioni fu l'Embbedding Theorem attribuito a Takens e Manè [Manè, Rand, Young, 1981; Takens, 1981]. La più importante conseguenza che ne deriva è che, sotto alcune ipotesi, è possibile ricostruire la dinamica del sistema multivariato utilizzando i valori ritardati nel tempo su una sola variabile. Lo spazio cosi ricostruito prende il nome di Embedded Phase Space. Dal punto di vista concettuale significa che nella evoluzione temporale di ogni singola variabile è contenuta l'influenza di tutte le altre. Gli studi si sono quindi concentrati su due problemi fondamentali: come identificare il tempo di ritardo (time lag) e come determinare la dimensionalità dello spazio. Uno dei maggiori apporti in questa direzione è stato dato da Abarbanel [Abarbanel, 1996] con una serie di funzioni e prescrizioni su come identificare questi parametri ed ottenere una corretta ricostruzione dell'attrattore.
Le invarianti della dinamica
Uno dei settori di sviluppo più importanti nell'analisi caotica è costituita dalla ricerca di invarianti della dinamica. Cioè di grandezze in grado di descrivere in modo ripetitivo il comportamento dinamico di un sistema. Queste quantità sono pensate come quantità statistiche di un sistema deterministico e sono invarianti rispetto alle condizioni iniziali. La ricerca in questo settore si è concentrata soprattutto su due caratteristiche: la dimensione frattale ed i coefficienti di Lyapunov che di seguito illustreremo.
La dimensione frattale è stata già incontrata nei precedenti paragrafi. Introdotta da Mandelbrot per caratterizzare le forme e legata agli attrattori da Lorenz [Lorenz, 1963], è stata ampiamente studiata per definire le modalità con cui il sistema si muove nello spazio delle fasi. Aldilà dei procedimenti matematici utilizzati per il calcolo [Grassberger, Procaccia, 1983; Casdagli, Sauer, Yorke, 1991], si può dire che la dimensione frattale rappresenta il modo in cui i punti dell'attrattore sono distribuiti nello spazio delle fasi. Sfortunatamente, mentre questa discriminante è molto utile per i sistemi teorici, il suo utilizzo per i sistemi reali è limitato dalla presenza di rumore esterno [Abarbanel, 1996].
L'altra invariante, meno sensibile al rumore, è il coeficiente di Lyapunov. In termini semplici si può dire che il coefficiente di Lyapunov esprime l'evoluzione nel tempo della distanza nell'attrattore tra due punti inizialmente vicini:
d(t) = d(to) e lambda(t-to)
dove lambda è il coefficiente di Lyapunov.
Nei sistemi regolari o pseudoperiodici questa distanza rimane costante o diminuisce (lambda negativo o nullo) mentre nei sistemi caotici diverge esponenzialmente (lambda positivo). Poiché il coefficiente di Lyapunov può essere visto anche come la tendenza alla divergenza delle orbite dell'attrattore, nei sistemi caotici il suo valore rappresenta il grado di caoticità del sistema. In questi termini può essere ridefinito anche il concetto di sistema caotico come un sistema caratterizzato da almeno un coefficiente di Lyapunov positivo (per un sistema non lineare a n gradi di libertà esistono n coefficienti di Lyapunov), cioè un sistema in grado di produrre informazione e generare entropia. (Rabinovich, 1978)
[...]
Caos e complessità
di Paola Cuneo
La possibilità che si possa prevedere con esattezza l'evoluzione nel tempo di un sistema in cui sono note tutte le forze agenti e le posizioni reciproche degli oggetti che lo compongono è ciò che gli scienziati chiamano determinismo. Da circa un secolo essi sanno che questa possibilità è irrealizzabile per la maggior parte dei sistemi a più oggetti in evoluzione. Esiste tutta una serie di fenomeni, detti caotici, per i quali previsioni di comportamento a lungo termine non sono possibili.
Per conoscere l'evoluzione di un sistema bisogna conoscerne le condizioni iniziali. Ma nessuna misura può avere una precisione assoluta: essa contiene sempre in sé un'incertezza. Sfortunatamente questa incertezza non rimane costante al passare del tempo e anzi non fa che aumentare.
I sistemi caotici presentano una grande "sensibilità alle condizioni iniziali": due situazioni di partenza molto simili (o che addirittura la precisione della nostra misura ci permette di considerare uguali) con il passare del tempo possono evolversi in modo molto differenziato. Da ciò consegue una forte irregolarità di comportamento. Tutto ciò che è veramente regolare è abbastanza prevedibile. Ma una grande sensibilità alle condizioni iniziali rende un sistema imprevedibile - dunque irregolare. Questo è quello che colloquialmente viene detto "effetto farfalla": quando una farfalla batte le ali a Tokio, può scatenarsi un uragano in Florida un mese più tardi, o, detto altrimenti, un dettaglio che inizialmente appare trascurabile, alla lunga può avere effetti importanti.
Il caos non è solamente un comportamento complicato e senza motivo apparente, il concetto è ben più sottile. Il caos ha le apparenze della complicazione ma la spiegazione è semplice: esso segue leggi deterministiche anche se appare disordinato e imprevedibile.
Attrattori strani
Lo studio dei fenomeni caotici è stato reso possibile dall'introduzione, poco più di un secolo fa, di una geometrizzazione della meccanica ad opera del matematico francese Henri Poincaré. Egli inventò il concetto di "spazio delle fasi", uno spazio matematico immaginario che rappresenta tutti i movimenti possibili di un sistema dinamico dato. Si può rappresentare lo stato di un sistema con un punto in un piano in un sistema di coordinate (non necessariamente spaziali, si tratta delle grandezze da cui dipende l'evoluzione del sistema). Se facciamo scorrere il tempo, le coordinate assumono valori diversi e il punto nel piano si sposta. Un punto che si sposta descrive una curva e questa curva è una rappresentazione del futuro dell'intero sistema. In realtà basta guardare la curva per vedere le caratteristiche dell'evoluzione di questo sistema, senza dover per forza considerare in dettaglio i valori numerici delle coordinate. Se per esempio la curva tende ad un certo punto e poi si ferma lì, ciò significa che il sistema raggiunge un punto di equilibrio da cui non si sposta più. Se la curva si chiude, vuol dire che il sistema si evolve con un ritmo periodico, assumendo a intervalli definiti gli stessi valori. Se scegliamo valori iniziali diversi, otteniamo una nuova curva: in questo modo possiamo vedere tutti i comportamenti possibili del sistema.
(a) Un punto fisso P nello spazio delle fasi rappresenta uno stato stazionario.
(b) Una curva chiusa rappresenta oscillazioni periodiche. Per semplicità qui lo spazio delle fasi è stato rappresentato bidimensionale.
Uno dei frutti dell'innovazione di Poincaré è che nello spazio delle fasi appaiono delle forme geometriche, dette attrattori, che permettono di visualizzare la dinamica del sistema. Facendo partire un sistema dinamico da un punto dato e considerando la sua evoluzione a lungo termine, si constata frequentemente che esso finisce per essere confinato in una certa regione dello spazio delle fasi. Per esempio un sistema che evolve verso un punto di equilibrio è un sistema con un attrattore e questo attrattore è il punto stesso. Un sistema che finisce per ripetere indefinitamente lo stesso ciclo, come può essere un pendolo che si muove senza attrito, ha un attrattore che è un anello. La dinamica dei sistemi a lungo termine è regolata dagli attrattori e la loro forma determina il tipo di dinamica che si produrrà.
La geometria del caos è piuttosto particolare: ad essa sono associati degli attrattori definiti strani, nell'intorno dei quali il movimento dettagliato non può essere determinato in anticipo. Questo è conseguenza dell'effetto farfalla. Pensate ad una pallina da ping-pong lanciata in un mare oleoso. Che la facciate cadere dall'alto o la lasciate andare sotto la superficie, essa si dirigerà verso la superficie. Una volta lì, seguirà una traiettoria complessa in mezzo alle onde, ma rimarrà in superficie, o per lo meno molto vicino ad essa, per quanto complessa sia questa traiettoria. La superficie del mare può essere una buona immagine di un attrattore strano.
Sui sistemi caotici si possono fare molte previsioni: per esempio si può distinguere un sistema caotico da un sistema realmente casuale. Spesso si può prevedere la forma di un attrattore, forma che non è modificata dall'effetto farfalla.
Determinismo e caos
La scoperta del caos ha rivelato la confusione fondamentale che esiste in noi fra le leggi e i comportamenti che queste leggi generano - confusione fra le cause e i loro effetti. Pensavamo che cause deterministe dovessero avere effetti regolari, ma ora vediamo che possono avere effetti molto irregolari, che possono essere confusi con effetti aleatori. Pensavamo che cause semplici producessero effetti semplici (e implicitamente che cause complesse avessero effetti complessi) ma ora sappiamo che cause semplici possono avere effetti complessi. Comprendiamo che conoscere le leggi e essere capaci di prevedere il futuro sono due cose diverse.
Questi risultati hanno trovato applicazioni in molteplici studi, i più noti dei quali riguardano la meteorologia e le previsioni del tempo, ma si sono verificate interessanti applicazioni del caos al battito cardiaco, alle onde elettroencefalografiche, alla dinamica delle popolazioni, al campo magnetico terrestre, alla traiettoria degli asteroidi del nostro sistema solare e dei satelliti artificiali, alle turbolenze intorno ad un sottomarino o un aereo, alla borsa e ai titoli finanziari…solo per fare alcuni esempi.
Mettere ordine nel caos
Negli ultimi decenni gli scienziati stanno studiando come "metter ordine" nel caos. I risultati indicano che il caos è quantificabile in modo preciso, esprimibile addirittura mediante un numero intero. Esiste pertanto una ben determinata gerarchia nel comportamento caotico: più è grande questo intero, più il caos del sistema è marcato. In secondo luogo hanno dimostrato anche sperimentalmente che il passaggio dall'ordine al caos avviene gradualmente per di più seguendo uno scenario invariabile, le cui singole tappe sono qualitativamente le stesse per i sistemi dinamici più disparati. L'analisi dettagliata di tale passaggio è il risultato di una felice sinergia di azione fra una profonda teoria matematica (la teoria KAM) ed i moderni metodi numerici e computazionali.
Oggi si ritiene che il caos, ancorché innescato da un'azione esterna (come la variazione delle condizioni iniziali), nasca in realtà dal sistema stesso: ordine e caos sono indissolubilmente legati e costituiscono due diverse condizioni di un soggetto (il sistema dinamico) in continua evoluzione.
Semplicità e complessità
Il caos ci ha insegnato che sistemi che obbediscono a regole semplici possono avere comportamenti complicati. Eppure per molti aspetti il mondo ci appare semplice. Questa semplicità tende a sparire quando si esaminano le cose in profondità, ma in superficie tuttavia esiste. Per non correre il rischio, nel procedere dell'investigazione scientifica, di perdere di vista questa semplicità, recentemente si sta facendo strada un approccio diverso ai fenomeni naturali: la "teoria della complessità". Più che di un modello scientifico vero e proprio si tratta soprattutto di una filosofia che investe il modo di studiare i fenomeni in campi delle scienze molto vari, come ad esempio la teoria dell'informazione, la biologia o le scienze sociali.
Complessità può essere definita in generale come la proprietà di un oggetto che contenga informazioni difficili da ottenere. Questa definizione si declina in modi diversi nelle varie applicazioni, ma l'idea che sta alla base della teoria della complessità è che, a grandi scale, da interazioni complesse di un gran numero di componenti emergono concetti semplici. Questa idea scaturisce dalla constatazione che molti sistemi disordinati fuori dall'equilibrio possono auto-organizzarsi per dare origine a strutture ordinate. In questo senso si può dire che la complessità si situa in mezzo fra l'ordine e il disordine.
Bibliografia
Ian Stewart, "Nature's numbers", Brockman Inc., 1995, capitoli VIII-IX; versione francese "La nature et les nombres", Hachette Littératures, 1998
David Ruelle "Caso e caos", Bollati Boringhieri, 1992
A. Vulpiani "Determinismo e caos", La Nuova Italia Scientifica, 1994
Peter H. Richter "Ordine e caos", Lettera Matematica n. 42, dicembre 2001
M. Mitchell Waldrop "Complexity: the emerging science at the edge of order and chaos", Simon and Schuster, 1992
La Teoria delle catastrofi
di Ernesto Salinelli
Introduzione
La matematica delle Catastrofi
Le applicazioni
Bibliografia
Introduzione
La matematica delle Catastrofi
Le applicazioni
Bibliografia
1 Introduzione
La Teoria delle Catastrofi viene alla luce negli anni 60’ ed è sostanzialmente associata al nome di René Thom. Tale teoria (accetteremo nel seguito tale appellativo senza ulteriori commenti), almeno nella versione cosiddetta "elementare", è riconosciuta dalla comunità dei matematici e catalogata nel Mathematics Subject Classification 2000 nella sezione 58Kxx, denominata "Teoria delle singolarità e teoria delle catastrofi". A fronte di una teoria matematica (difficile e) consolidata, l’aspetto sicuramente più controverso delle "catastrofi" ha riguardato le sue applicazioni, attorno alle quali si è acceso un forte dibattito che si è protratto fin verso la metà degli anni '80 (si veda ad esempio Tonietti 1983). Successivamente l’interesse per tale teoria è andato in parte scemando. Una stima, sia pur grossolana, dell’impatto della teoria delle catastrofi nella comunità scientifica si può ottenere comunque spulciando il catalogo del MathScinet e confrontandosi con altre teorie spesso (impropriamente a parere di chi scrive) accomunate alla teoria delle catastrofi: una ricerca mediante la parola chiave "catastrophe theory" produce, dal 1971 ad oggi, un elenco di 509 lavori, a fronte dei 5119 ottenuti sullo stesso periodo inserendo la parola chiave "chaos" e dei 12336 ottenuti con "bifurcation".
Nelle poche righe che seguono cercheremo di dare un rapido "assaggio" di ciò che la teoria delle catastrofi rappresenta sia dal punto di vista "teorico" sia dal punto di vista "applicativo". Rimandiamo per presentazioni più rigorose ed esaustive alla bibliografia essenziale che il lettore incontrerà alla fine di queste righe.
2 La matematica delle Catastrofi
L’idea alla base del calcolo differenziale in una variabile reale è, come noto, quella di cercare una rappresentazione locale di una funzione mediante una funzione lineare; in termini "geometrici" una funzione reale di variabile reale f si dice differenziabile in un punto x0 interno al suo dominio se il suo grafico risulta localmente "bene approssimato" dalla retta tangente ad esso nel punto di coordinate (x0, f (x0)), retta la cui pendenza è data dalla derivata prima f'(x0). Data una funzione differenziabile, lo studio di ciò che capita muovendosi “di poco” dal punto x0 può essere condotto considerando i valori corrispondenti sulla retta tangente (facilmente deducibili) in alternativa a quelli del grafico della funzione stessa (in generale difficilmente deducibili). Tale procedura funziona bene a patto che la retta tangente non sia orizzontale: se ciò avviene, cioè se f'(x0)=0, l’andamento locale della funzione non viene catturato nemmeno approssimativamente dalla retta tangente dato che questa esprime il grafico di una funzione costante (vedi Figura 1).
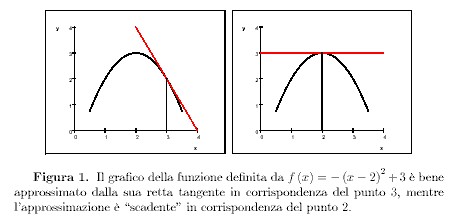
In corrispondenza dei punti "problematici", cioè quelli a tangente orizzontale, detti punti critici o singolari, si cerca di rappresentare (se possibile) una funzione mediante espressioni polinomiali di grado superiore al primo, che coinvolgono (e quindi bisogna a priori chiederne l'esistenza) le derivate successive della funzione (nell'esempio precedente basta ovviamente la derivata seconda). Per poter affrontare una qualsiasi situazione si può arrivare a chiedere ad f di possedere tutte le derivate cioè di essere liscia. Come è noto, in tal caso ci si può chiedere se la serie che raccoglie tutte le derivate della funzione f nel punto x0 (nota come serie di Taylor) permetta di dedurre i valori della funzione, cioè se (e dove) valga l'uguaglianza:
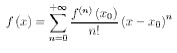
A tale approccio, di natura globale, si può contrapporre il seguente, di natura locale: data una funzione1 liscia nel punto x0 ci si chiede se esista un cambio di coordinate (locale) che permetta di riscrivere la funzione come il suo primo termine non nullo della sua serie di Taylor. L'approccio è ovviamente qualitativo, non numerico: l'idea è che gli elementi essenziali che caratterizzano l'andamento di una funzione siano contenuti nell’insieme delle sue singolarità, che ne rappresentano, con abuso di linguaggio, il suo "patrimonio genetico". Risulta così interessante poter classificare le funzioni lisce in termini delle loro singolarità, sia per quanto riguarda il numero, sia per quanto riguarda la loro tipologia. Per poter comprendere il senso di tale classificazione è necessario ancora un piccolo sforzo per cogliere un ulteriore aspetto del problema. Se torniamo all'esempio illustrato in Figura 1, possiamo tracciare il grafico della derivata prima f' della funzione f .
(Tecnicamente, dato che ci occupiamo di un’analisi locale, si dovrebbe parlare di germe).
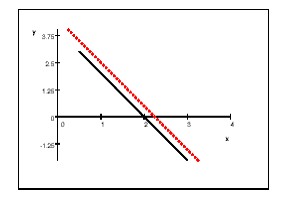
Figura 2. Grafico della funzione definita da f'(x) = -2(x - 2)
Si osserva allora che il punto singolare x0 = 2 corrisponde al punto in cui il grafico della funzione derivata prima (in nero in Figura 2) interseca l'asse delle ascisse. Notiamo ora che, se "perturbiamo di poco" tale grafico (ottenendo, ad esempio, il grafico in rosso), l’intersezione resta (sia pur numericamente differente dalla precedente) qualitativamente invariata.
Consideriamo ora la funzione definita (su R) da g (x) = x3. Il punto x=0 è un punto singolare (cioè g'(0)=0), più precisamente un punto singolare degenere dato che si ha anche f''(0)=0 (in contrapposizione, casi come quello della funzione f si dicono singolarità non degeneri). Si può notare (vedi Figura 3) che piccole perturbazioni del grafico della sua derivata prima g' cambiano drasticamente la situazione per quanto riguarda la presenza di singolarità.
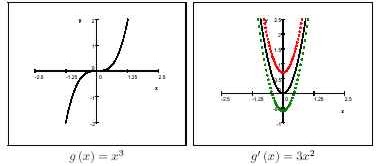
Figura 3. Grafici di g (x) = x3 e della sua derivata prima
Come illustrato in Figura 4., il punto singolare x=0 (punto di flesso a tangente orizzontale) a seguito di una "piccola perturbazione" o scompare (grafico in rosso), dando luogo ad una funzione senza singolarità, oppure "si duplica" (grafico in verde), dando luogo ad una funzione che presenta due punti singolari (un punto di massimo e uno di minimo).
(Le piccole perturbazioni alle quali si fa spesso riferimento in linguaggio più tecnico ed appropriato si chiamano germi di diffeomorfismi locali.)

Figura 4. Una "piccola perturbazione" della funzione g dà origine a nuove funzioni senza punti singolari (grafico in rosso) oppure con due punti singolari (grafico in verde).
In conclusione: esistono "funzioni" che sono strutturalmente stabili, nel senso che piccole perturbazioni non ne cambiano i punti singolari ed il loro tipo. Ciò viene catturato dal modo in cui (in dimensione 1) il grafico della derivata prima taglia l’asse delle ascisse. Dunque, la funzione f presenta un punto singolare strutturalmente stabile, la funzione g instabile. In generale, ci si potrebbe anche spingere ad affermare che la funzione f è generica mentre tale non è il caso della funzione g. Tuttavia, notiamo che se si perturbano di poco i grafici in Figura 4 la loro fisionomia non cambia (vedi Figura 5). Dunque, se è vero che y=x3 presenta una singolarità instabile, la sua versione "perturbata" y=x3+ax, al variare del parametro a, risulta strutturalmente stabile.
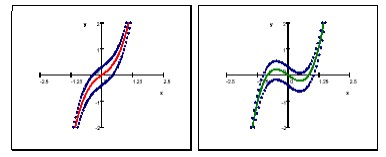
Figura 5. Piccole perturbazioni dei casi senza singolarità o con due singolarità non ne modificano l’andamento qualitativo locale.
L’essenza del famoso teorema di classificazione di Thom (a cui si riconduce la congettura nel 1963 alla quale seguono i contributi di Malgrange nel 1965 e di Mather 1967) sta proprio nel dimostrare, sotto certe condizioni, la possibilità di classificare le singolarità, dette centri organizzatori della catastrofe, di funzioni lisce immergendole nei corrispondenti spiegamenti universali che risultano strutturalmente stabili. A ciascuna situazione si associa un nome evocativo cui ci si riferisce per distinguere le sette tipologie, note come le sette catastrofi elementari. Riportiamo di seguito l’elenco di tali forme:
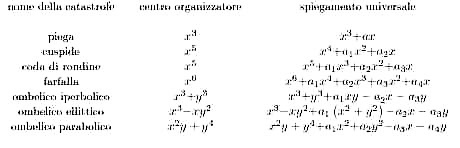
3 Le applicazioni
Negli scritti di Thom si trovano le idee generali che ispirano il suo lavoro matematico, idee che nascono dall’osservazione dei fenomeni naturali. Per Thom la natura è un catalogo di forme che nascono, entrano in conflitto fra loro, muoiono in un continuo divenire. Una particolare forma (di una foglia, di una pietra, di un essere vivente) per poter essere individuata deve essere stabile: piccole perturbazioni non ne devono modificare le caratteristiche essenziali. Dunque, le forme hanno una loro dinamica ed accanto ai domini di stabilità si osservano situazioni nelle quali piccole modifiche provocano grandi effetti: la morfogenesi si occupa di studiare tali processi e i cambiamenti di forma vengono denominati catastrofi (dal greco che significa girare giù, cambiamento, rovesciamento). La classificazione delle forme elementari risulta così possibile imponendo non solo la stabilità delle forme ma anche la stabilità del processo di cambiamento.
Non possiamo addentrarci nel complesso e controverso mondo delle applicazioni della teoria delle catastrofi: ci limiteremo quindi a presentare, sia pur per sommi capi, la catastrofe che più ha avuto successo nelle applicazioni (mostrando un esempio di natura economica), la cuspide, rimandando alla letteratura il lettore più interessato. Prima, però, segnaliamo un aspetto che potrebbe sembrare curioso: sorprendentemente, le "applicazioni delle catastrofi" non sono sostanzialmente associate al nome di Thom ma principalmente a quello del matematico inglese Cristopher Zeeman e della sua scuola (la cosiddetta "scuola inglese") che, nella seconda metà degli anni 70’, ha prodotto applicazioni di ogni genere inerenti le caustiche, le transizioni di fase liquido/gas, problemi di elasticità, fino a giungere a quelle sul battito cardiaco, i crolli di borsa, le rivolte nelle carceri, lo scoppio di guerre.
Il cosiddetto modello a cuspide si può incontrare quando si prendono in considerazione una variabile di stato (z) e due variabili di controllo (x, y): in uno spazio a tre dimensioni si rappresenta la superficie, detta superficie di comportamento, dei punti singolari del sistema analizzato (vedi Figura 6).
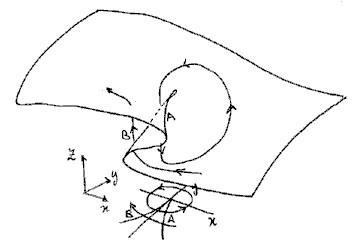
Figura 6. Il modello a cuspide
La denominazione di cuspide deriva dal fatto che se si proiettano sul piano delle variabili di controllo i punti della superficie in corrispondenza dei quali il piano tangente risulta verticale, si ottiene proprio una cuspide (vedi Figura 6). Sulla superficie di comportamento sono possibili vari movimenti in funzione dei valori che assumono le variabili di controllo: i principali sono descritti in Figura 7.
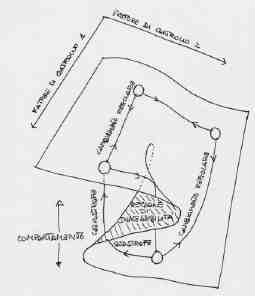
Figura 7 Possibili movimenti sulla superficie di comportamento
Il "salto catastrofico" avverrà in punti differenti a seconda che si adottino rispettivamente la regola di Maxwell (proposta da Thom) oppure la regola del ritardo (proposta da Zeeman). Senza entrare nei particolari segnaliamo che la prima prevede che il salto catastrofico avvenga prima di aver raggiunto il bordo della piega, la seconda prevede che il salto catastrofico avvenga solo raggiunto il bordo della piega. L’analisi della Figura 7. ci consente di osservare ancora due caratteristiche del modello a cuspide: da una parte la presenza di una regione di inacessibilità corrispondente a punti singolari instabili; dall’altra osserviamo un fenomeno di isteresi, cioè la transizione dal piano superiore a quello inferiore non avviene nello stesso punto in cui avviene quella dal piano inferiore a quello superiore (vedi Figura 8).

Figura 8. Fenomeno dell’isteresi nel modello a cuspide
Infine, il modello permette di analizzare situazioni di bimodalità, ossia situazioni in cui, a parità di combinazioni delle variabili di controllo, si possono determinare due diverse reazioni di comportamento della variabile di stato, localizzate rispettivamente sul piano inferiore e su quello superiore della piega (vedi Figura 9).
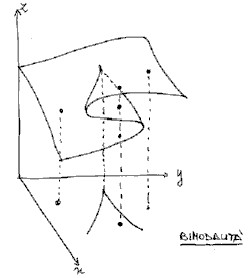
Figura 9. Bimodalità nel modello a cuspide
Zeeman ha proposto l’utilizzo del modello a cuspide per la spiegazione dei crolli di borsa. Si suppone che agiscano due tipi di soggetti, coloro che agiscono sulla base delle informazioni di natura economica (politica economica, monetaria, fiscale, analisi dei bilanci, ecc.) e coloro che agiscono solo a fini speculativi. Le variabili di controllo sono quindi l’ammontare delle azioni possedute dai due gruppi contrapposti. In realtà le due variabili di controllo hanno una valenza differente: con riferimento alla Figura 7, il fattore di controllo 2 in generale si dice fattore normale, il fattore 1 si dice fattore separante e tale distinzione terminologica è motivata dal fatto che solo in presenza del fattore separante può avvenire il "salto" dalla faccia inferiore a quella superiore (o viceversa) della superficie. La variabile di stato nel nostro esempio è la variazione dell’indice di borsa (ad esempio, del MIBTEL). Come si può dedurre dall’analisi della Figura 7, in assenza di speculazione la domanda conduce al rialzo; alternativamente, la presenza di capitali speculativi farà sì che variazioni della domanda possano portare a brusche variazioni (catastrofi) dell’indice di borsa.
4 Bibliografia essenziale
[1] Arnol’d V.I., Teoria delle catastrofi, Bollati Boringhieri, 1990
[2] Brambilla F., Guerraggio A., Salinelli E., Teoria delle catastrofi e applicazioni economiche, Studi Matematici n.5, Istituto di Metodi Quantitativi, Università "L. Bocconi", 1988
[3] Bröcker T., Di.erentiable germs and catastrophes, Cambridge University Press, 1975
[4] Galeotti M., Gori F., Un modello geometrico per le configurazioni di equilibrio della bilancia commerciale. Catastrofi e stabilità del tasso di cambio, preprint del Centro di Analisi Globale del CNR, 1980
[5] Gilmore S., Catastrophe theory for scientists and engeneers, Wiley, 1981
[6] Lu Y.-C-, Singularity theory and an introduction to catastrophe theory, Springer-Verlag, 1976
[7] Marmo G., Vitale B., La teoria delle catastrofi, Sapere, 804, 1977, pp. 17-28
[8] Pietrabissa E., Un possibile utilizzo della teoria delle catastrofi nella costruzione di modelli econometrici, Rivista di Statistica Applicata, Vol.12, No.3, 1979
[9] Pomian K., Catastrofi, in Enciclopedia Einaudi, 2, 1977, pp. 789-803
[10] Poston T., Stewart I., Catastrophe theory and its applications, Pitman, 1978
[11] Thom R., Stabilità strutturale e morfogenesi. Saggio di una teoria generale dei modelli, Einaudi,
1980 [12] Tonietti T., Catastrofi. Una controversia scientifica, Ed. Dedalo, 1983
[13] Zeeman E.C., La teoria della catastrofe, Le Scienze, 96, 1976, pp. 16-29
[14] Zeeman E.C., Catastrophe theory. Selected-Papers 1972-1977, Addison Wesley, 1977
[15] Woodcock A., Davis M., La teoria delle catastrofi, Garzanti, 1982